补码运算有什么特点

补码运算的特点有：1、符号位与数值位统一处理；2、简化运算器结构；3、方便实现溢出检测；4、简化乘除运算；5、运算结果唯一；6、便于实现二进制数的加减运算；7、抗干扰能力强；8、与原码和反码相比优势明显。

补码运算的特点

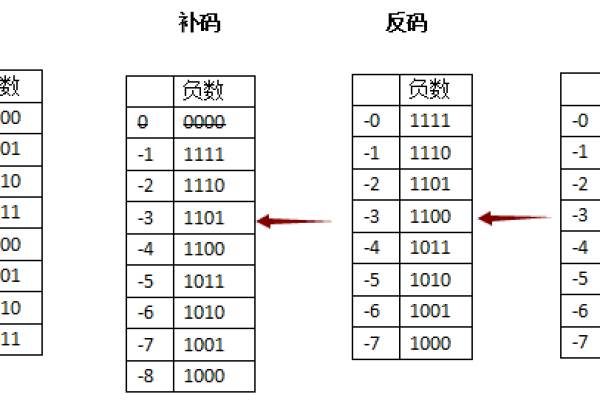
补码是一种计算机内部使用的表示有符号整数的方法，它是基于二进制的一种运算方式，补码运算具有以下特点：

1、加法具有反向性质

加法的反向性质是指，对于任何两个有符号整数a和b,都有(-a) + b = -(a + b)，这意味着，当我们对一个数进行加法运算时，实际上是在计算这个数与0之间的差值，对于3和5,它们的和是8,而8减去3等于5,再减去5等于0，我们可以得出结论：3 + 5 = -(5 + 3)。

2、减法具有反向性质

减法的反向性质与加法相同，即对于任何两个有符号整数a和b,都有(-a) b = -(a b)，这意味着，当我们对一个数进行减法运算时，实际上是在计算这个数与0之间的差值，对于5和3,它们的差是2,而2减去5等于-3,再加上3等于0，我们可以得出结论：5 3 = -(3 5)。

3、溢出不会引起进位

在补码表示法中，当一个数的最高位(符号位)为1时，表示这是一个负数，当一个数加1后，最高位变为0,此时称这个数发生了溢出，在补码表示法中，溢出不会引起进位，对于-7(二进制表示为1111111)来说，它加1后变为-6(二进制表示为1111110),没有发生进位，这是因为在补码表示法中，溢出被看作是一个特殊的加法操作，它只改变了最高位的值，而不会影响其他位的值。

4、有符号整数的加法和减法可以直接通过二进制位移实现

在补码表示法中，有符号整数的加法和减法可以直接通过二进制位移实现，具体来说，对于两个有符号整数a和b(假设它们的符号相同),它们的和c可以通过以下步骤计算：

(1) 如果a < b,则c = a + (b << (sizeof(int) * 8 1))

(2) 如果a >= b,则c = a (b << (sizeof(int) * 8 1))

这里的关键是位移操作符<<,它将一个数的所有二进制位向左移动指定的位数，对于8位整数i来说，i << n表示将i的所有二进制位向左移动n位，由于补码中的每个二进制位都代表一个权重因子(2的幂次方),因此通过位移操作可以方便地实现加法和减法运算。

相关问题与解答

1、为什么补码表示法比原码表示法更节省存储空间？

答：原码表示法中，正数和负数都需要用两个字节来表示，在补码表示法中，正数只需要用一个字节来表示(因为最高位是0),而负数则需要用三个字节来表示(因为最高位是1)，这样一来，补码表示法就可以节省至少一半的存储空间，由于补码中的溢出不会引起进位，因此还可以避免一些潜在的问题。

2、在补码表示法中，如何判断一个数是正数还是负数？

答：在补码表示法中，可以通过检查一个数的最高位(符号位)来判断它是正数还是负数，如果最高位为0,则这个数是正数；如果最高位为1,则这个数是负数，需要注意的是，这种方法只能用来判断有符号整数的正负性，对于无符号整数来说是没有意义的。