c语言3个数最小公倍数怎么求

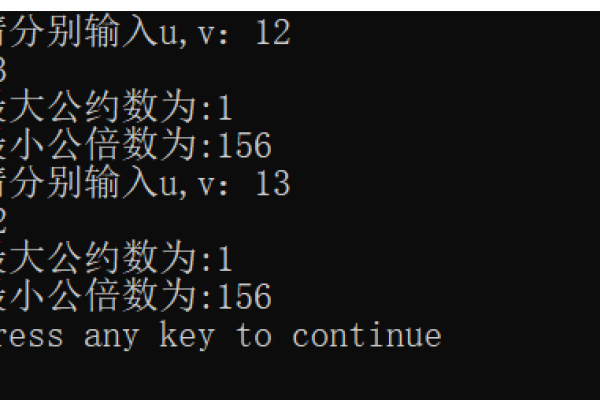
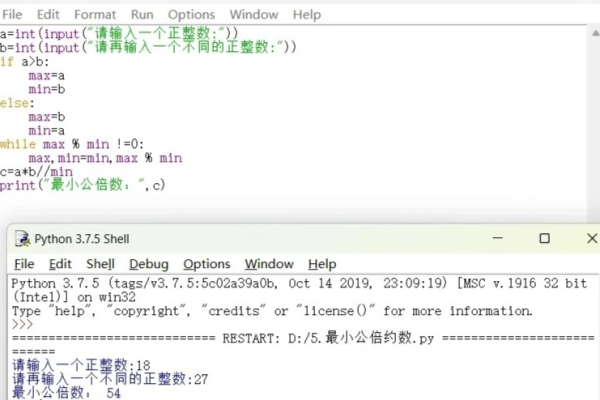
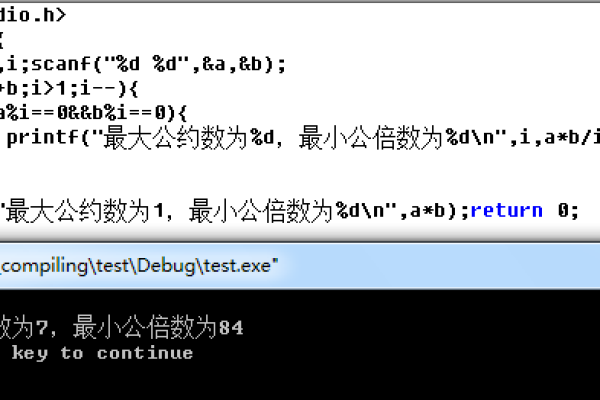
要求三个数的最小公倍数，可以使用以下步骤：

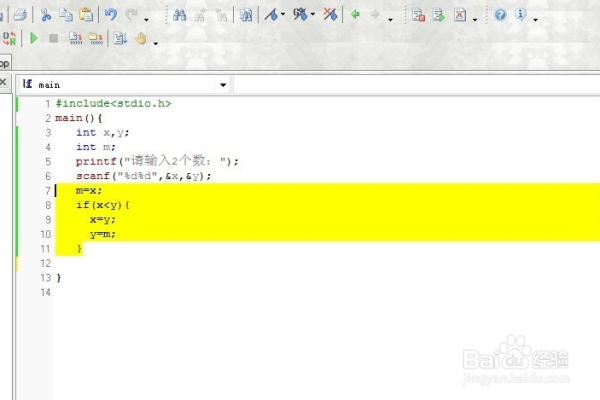
1、找出这三个数的所有质因数。

2、对于每个质因数，选择在三个数中出现次数最多的那个数作为该质因数的幂次。

3、将选出的质因数按照幂次相乘，得到的结果就是这三个数的最小公倍数。

下面是一个使用C语言实现的示例代码：

#include <stdio.h>
// 判断一个数是否为质数
int is_prime(int num) {
    if (num <= 1) {
        return 0;
    }
    for (int i = 2; i * i <= num; i++) {
        if (num % i == 0) {
            return 0;
        }
    }
    return 1;
}
// 计算最大公约数
int gcd(int a, int b) {
    while (b != 0) {
        int temp = a % b;
        a = b;
        b = temp;
    }
    return a;
}
// 计算最小公倍数
int lcm(int a, int b) {
    return a * b / gcd(a, b);
}
// 扩展欧几里得算法求最大公约数和最小公倍数
void extended_gcd(int a, int b, int *result_gcd, int *result_lcm) {
    if (b == 0) {
        *result_gcd = a;
        *result_lcm = a;
        return;
    }
    extended_gcd(b, a % b, result_gcd, result_lcm);
    int temp_gcd = *result_gcd;
    int temp_lcm = *result_lcm;
    *result_gcd = temp_gcd (a / b) * temp_gcd;
    *result_lcm = temp_lcm / b * (temp_gcd (a / b) * temp_gcd);
}
int main() {
    int num1, num2, num3;
    printf("请输入三个整数：");
    scanf("%d %d %d", &num1, &num2, &num3);
    int result_gcd, result_lcm;
    extended_gcd(num1, num2, &result_gcd, &result_lcm); // 计算最大公约数和最小公倍数（num1和num2）
    extended_gcd(result_gcd, num3, &result_gcd, &result_lcm); // 计算最大公约数和最小公倍数（前两个结果和num3）
    printf("最小公倍数为：%d
", result_lcm);
    return 0;
}

这个程序首先定义了is_prime函数来判断一个数是否为质数，然后定义了gcd函数来计算两个数的最大公约数，接着定义了lcm函数来计算两个数的最小公倍数，通过extended_gcd函数实现了扩展欧几里得算法，可以同时计算出最大公约数和最小公倍数，在main函数中，用户输入三个整数，然后调用extended_gcd函数计算它们的最小公倍数并输出结果。