点数模拟浮点_模拟案例
- 行业动态
- 2024-07-08
- 3977
点数模拟浮点是一种计算机科学中用于表示实数的近似方法,其中数字被分成整数和小数部分。通过这种方法,可以有效地处理非常大或非常小的数值,同时保持计算的准确性和效率。
在计算机科学中,浮点数的表示和运算是基础且关键的内容,与定点数不同,浮点数通过牺牲一定的精度来获得更大范围的数值表示,在某些没有专门硬件支持浮点运算的系统中,使用定点数模拟浮点数成为一种可行的方案,这种模拟不仅对于理解浮点数的基本原理具有重要意义,而且在实际工程应用中也具有广泛的实用价值。
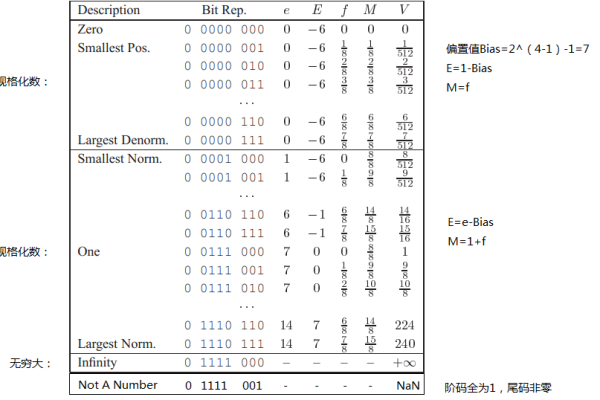
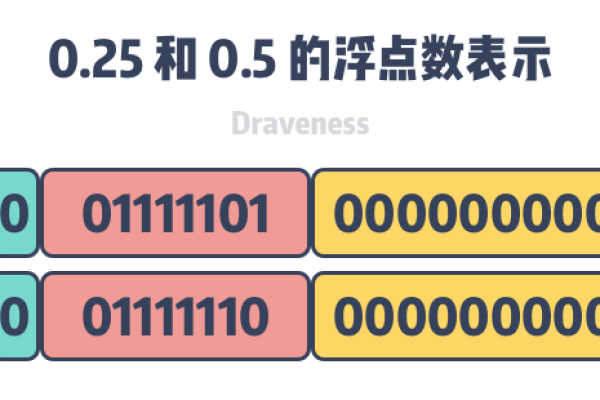
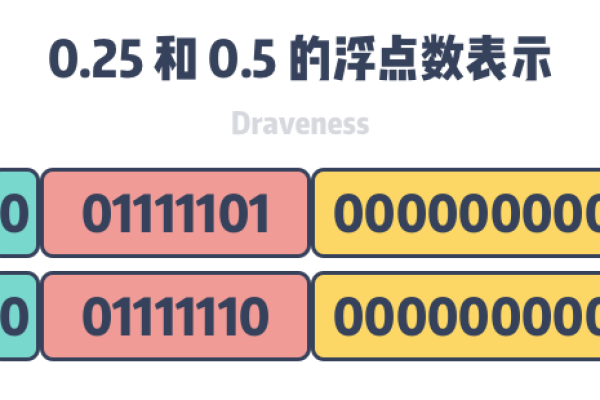
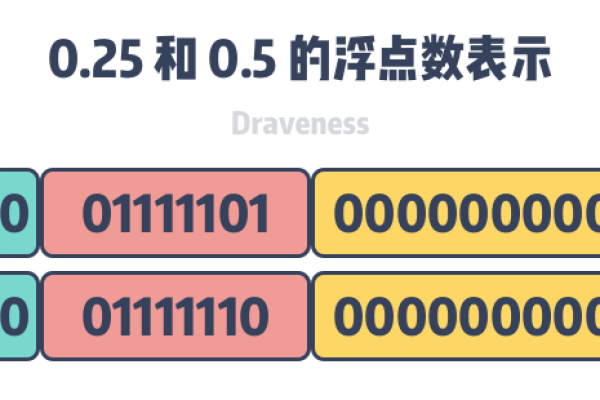
定点数模拟浮点数的核心在于将浮点数的表示方式转化为定点数能够处理的形式,这涉及到几个关键步骤,包括编码转换、运算模拟以及结果的解码,浮点数被分解为符号位、阶码和尾数三个部分,阶码用于确定浮点数的范围,而尾数则决定数值的精度,在模拟过程中,阶码通常通过定点数的移位操作来实现其对数值范围的调整,而尾数则直接参与四则运算。
除法转换为乘法或移位运算是定点数模拟浮点数运算的一个常见策略,在浮点表示中,除法往往需要复杂的算法来实现,尤其是规格化数的除法,通过将除法转换为乘法或者移位运算,可以有效简化计算过程,提高运算效率,一个浮点数除以2的操作,可以通过将该数的二进制表示向右移动一位来实现,相当于阶码减小,而尾数保持不变。
在没有硬件支持的情况下,软件模拟浮点数运算提供了另一种实现途径,这种方法主要依赖于高级语言或者底层编程技巧来实现浮点数的表示和运算规则,软件模拟的优势在于其灵活性高,可以根据不同的应用需求设计特定的模拟策略,这也意味着开发者需要对浮点数的运算规则有深入的理解,包括如何处理溢出、下溢、舍入等问题。
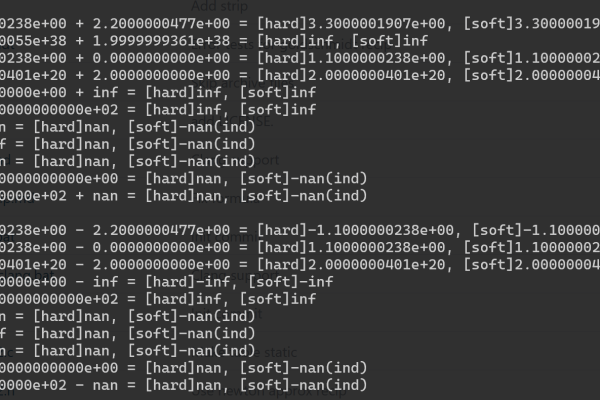
测试与验证是确保模拟准确性的重要环节,通过设计一系列的测试案例,可以验证模拟程序的正确性,这些测试不仅要覆盖正常的运算情况,还要考虑到异常情况,如极端值、特殊值等,通过与标准浮点数运算的结果进行比较,可以评估模拟程序的准确性和可靠性。
科学计算是浮点数模拟的另一个重要应用领域,在科学研究和工程技术中,经常需要进行大量的数值计算,而这些计算往往涉及到浮点数,在缺少硬件支持的环境中,通过软件模拟浮点数运算,可以有效地支持科学计算的需求,这对于提升计算效率、降低成本具有重要意义。
使用定点数模拟浮点数也存在一些局限性,最明显的限制来自于精度的损失,由于定点数的位数有限,模拟浮点数时可能无法精确表示所有浮点数的值,特别是那些很小或者很大的数,模拟过程中的运算复杂度也是一个不容忽视的问题,相比于直接的硬件运算,软件模拟往往需要更多的计算步骤,这可能会导致性能下降。
尽管定点数模拟浮点数在某些情况下非常有效,但在设计模拟程序时仍需谨慎,开发者需要全面考虑模拟策略的选择、精度的控制以及性能的优化,对于特定应用场景,还需要根据实际需求进行详细的分析和测试,以确保模拟程序既高效又准确。
相关问答FAQs
Q1: 浮点数模拟中如何处理精度损失问题?
A1: 精度损失是浮点数模拟中常见的问题,一种有效的处理方法是在软件层面引入更高精度的数据类型来进行运算,例如使用64位的定点数来模拟32位的浮点数,另一种方法是采用更精细的舍入策略,比如在每次运算后根据情况进行适当的舍入操作,以减少累积误差。
Q2: 如何优化浮点数模拟的性能?
A2: 优化浮点数模拟的性能可以从几个方面入手,首先是算法优化,比如采用查找表来加速某些复杂运算的执行,其次是减少不必要的计算,例如在进行加法运算时可以先对齐阶码,避免每次运算都进行阶码调整,可以考虑利用并行计算资源,如多核CPU或者GPU,来加速大规模的浮点运算任务。
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/343886.html