偏度和峰度,如何理解这两个统计学中的重要概念?
- 行业动态
- 2024-11-24
- 1
偏度和峰度是描述数据分布形态的两个统计量,分别反映数据的对称性和尖峭程度。
在统计学中,偏度和峰度是描述数据分布形态的两个重要指标,偏度反映了数据分布的不对称性,而峰度则描述了数据分布顶端尖峭或平坦的程度,这两个统计量对于理解数据集的特征至关重要,它们可以帮助分析师判断数据是否服从正态分布,以及分布的尾部特性。
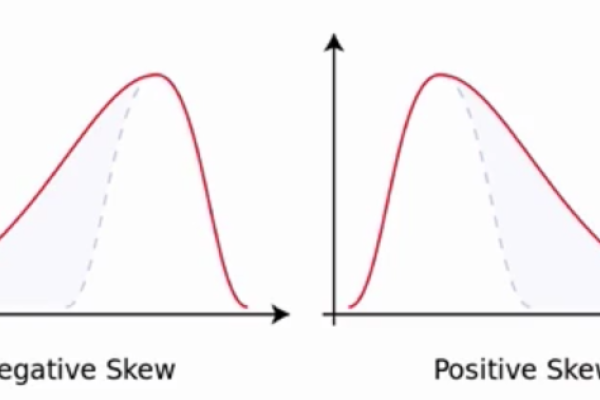
偏度(Skewness)是指数据分布的不对称程度,一个分布的偏度为零意味着它是对称的,也称为正态分布,正偏度表示分布的尾部向右延伸,即数据中有较多的极端大值;负偏度则表示分布的尾部向左延伸,即数据中有较多的极端小值,偏度的计算公式为:
$$
\text{Skewness} = \frac{n}{(n-1)(n-2)} \sum_{i=1}^{n} \left(\frac{x_i \bar{x}}{s}\right)^3
$$
$n$ 是样本大小,$x_i$ 是第 $i$ 个观测值,$\bar{x}$ 是样本均值,$s$ 是样本标准差。
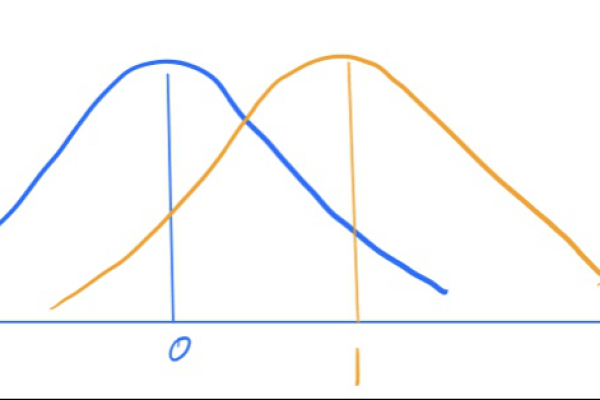
峰度(Kurtosis)是描述数据分布顶端尖峭或平坦的度量,正态分布的峰度定义为3,峰度大于3表示分布比正态分布更尖锐,有更多的极端值;峰度小于3表示分布比正态分布更平坦,极端值较少,峰度的计算公式为:
$$
\text{Kurtosis} = \frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i=1}^{n} \left(\frac{x_i \bar{x}}{s}\right)^4 \frac{3(n-1)^2}{(n-2)(n-3)}
$$
为了更直观地展示偏度和峰度,我们可以通过表格来比较不同数据集的这两个统计量,假设我们有三个数据集A、B和C,它们的偏度和峰度如下表所示:
| 数据集 | 偏度 (Skewness) | 峰度 (Kurtosis) |
| A | 0.5 | 3.2 |
| B | -0.8 | 2.5 |
| C | 0.0 | 4.0 |
从表中可以看出,数据集A呈现出轻微的正偏态,且峰度略高于正态分布,这意味着A的分布比正态分布稍微尖锐一些,数据集B显示出负偏态,且峰度低于3,表明B的分布比正态分布更平坦,极端值较少,数据集C的偏度为0,峰度为4,这表明C的分布是对称的,但比正态分布更尖锐,有更多的极端值。
了解偏度和峰度对于数据分析非常重要,因为它们可以揭示数据的潜在特征,影响分析结果的解释和决策,在金融领域,资产收益率的偏度和峰度可以帮助投资者评估风险和制定投资策略,在医学研究中,生物标志物的偏度和峰度可能与疾病的严重程度或治疗效果有关。
FAQs:
Q1: 偏度和峰度如何影响我们对数据分布的理解?
A1: 偏度和峰度提供了数据分布形状的信息,偏度告诉我们分布是否对称,以及极端值偏向哪一侧;峰度告诉我们分布顶端的尖锐程度,这些信息有助于我们判断数据是否适合某些统计分析方法,或者是否需要对数据进行转换以满足特定分析的需求。
Q2: 如果一个数据集的偏度和峰度都接近于正态分布的值,这意味着什么?
A2: 如果一个数据集的偏度接近于0,峰度接近于3,这通常意味着数据近似服从正态分布,正态分布是许多统计测试和模型的基本假设,因此这样的数据集在进行参数估计和假设检验时可能会更加可靠,即使偏度和峰度接近理想值,也需要通过其他统计测试(如正态性检验)来进一步验证数据的正态性。
小伙伴们,上文介绍了“偏度和峰度”的内容,你了解清楚吗?希望对你有所帮助,任何问题可以给我留言,让我们下期再见吧。
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/343446.html