Ceil函数是什么？它有哪些用途和特性？

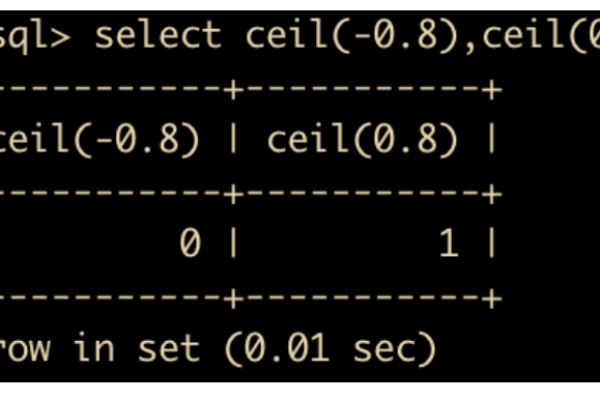
“ceil” 是一个数学函数，用于向上取整，即返回大于或等于指定数值的最小整数。

Ceiling函数是数学中一个非常实用的工具，它能够帮助我们将一个数字向上取整到最接近的整数，无论是在学术研究、工程设计还是日常生活中，ceiling函数都有着广泛的应用，本文将深入探讨ceiling函数的定义、性质、应用场景以及如何在实际问题中运用这一工具。

一、Ceiling函数的定义与基本性质

1. Ceiling函数的定义

Ceiling函数，记作⎛⎝ceil(x)⎞⎠，是指对于任意实数x，返回大于或等于x的最小整数，形式化地，可以表示为：

[ ceil(x) = lceil x rceil ]

2. 基本性质

单调性：ceiling函数是一个单调递增函数，即如果 ( x_1 < x_2 )，( lceil x_1 rceil leq lceil x_2 rceil )。

整数输入：当x为整数时，( lceil x rceil = x )。

非负性：对于所有非负实数x，( lceil x rceil geq 0 )。

与floor函数的关系：( lceil -x rceil = lfloor -x rfloor )，其中floor函数是向下取整函数。

二、Ceiling函数在不同领域的应用

1. 计算机科学

在编程和算法设计中，ceiling函数常用于确定循环次数、数组大小等，在处理需要按块分配内存的问题时，ceiling函数可以帮助计算所需块的数量。

2. 金融数学

在金融领域，ceiling函数可用于计算贷款分期付款中的期数，或者确定投资回报率达到某一目标所需的最短时间。

3. 工程与物理

在工程学中，ceiling函数可用于估算材料需求、优化资源分配等，在建筑设计中，可能需要根据房间面积向上取整以确定所需地板砖的数量。

4. 统计学与概率论

在统计分析中，ceiling函数可用于数据分组、四舍五入等操作，以便更好地分析数据分布特性。

三、Ceiling函数的计算方法与实例

1. 手动计算

对于简单的数值，可以直接通过观察或简单计算得到结果，( lceil 3.2 rceil = 4 )，因为4是大于3.2的最小整数。

2. 编程语言实现

许多编程语言都提供了内置的ceiling函数或类似的库函数，以下是一些常见语言中的实现方式：

Python：使用math模块中的math.ceil()函数。

Java：使用Math类中的Math.ceil()方法。

JavaScript：可以使用Math.ceil()函数。

3. 实例分析

假设有一个项目需要购买木材，每根木材的长度为2米，而项目总共需要5.5米的木材，为了确保有足够的木材完成项目，我们需要计算至少需要多少根木材，使用ceiling函数，我们可以得出：

[ lceil frac{5.5}{2} rceil = lceil 2.75 rceil = 3 ]

至少需要购买3根木材。

四、Ceiling函数的高级应用与技巧

1. 结合其他数学函数

Ceiling函数可以与其他数学函数结合使用，以解决更复杂的问题，结合log函数可以计算对数的上限，结合sqrt函数可以估算平方根的上界等。

2. 优化算法中的应用

在优化算法中，ceiling函数可用于确定迭代次数、步长调整等，以提高算法的效率和精度。

五、Ceiling函数的局限性与注意事项

尽管ceiling函数在很多场合都非常有用，但也有一些局限性需要注意：

精度问题：对于非常大的数值或非常小的差异，直接使用ceiling函数可能会导致精度损失。

上下文依赖：在某些特定应用场景下，直接向上取整可能不是最佳选择，需要结合实际情况进行调整。

Ceiling函数作为数学中的一个基本工具，其简单而强大的功能在各个领域都有着广泛的应用，通过深入理解和灵活运用ceiling函数，我们可以更好地解决实际问题，提高工作和学习的效率，希望本文能够为大家提供一个关于ceiling函数的全面视角，并激发更多关于其在各领域应用的思考和探索。

FAQs

Q1: 为什么有时候我们需要使用ceiling函数而不是直接四舍五入？

A1: 虽然四舍五入在某些情况下是一个合理的选择，但在需要确保结果总是大于或等于原始数值的场景下（如资源分配、预算控制等），ceiling函数提供了一种更为保守和安全的取整方式，它确保了无论原始数值的小数部分是多少，结果都会向上取整到最接近的整数，从而避免了因四舍五入导致的低估。

Q2: 如何在没有现成函数的情况下手动计算ceiling函数的值？

A2: 如果没有一个现成的ceiling函数可用，你可以通过以下步骤手动计算：确定给定数值的小数部分；检查小数部分是否大于零；如果是，则将整数部分加一作为结果；如果不是（即小数部分为零或负数），则直接返回整数部分作为结果，这种方法虽然不如直接调用函数高效，但在理解ceiling函数工作原理的同时，也能作为一种备用方案。

以上内容就是解答有关“ceil”的详细内容了，我相信这篇文章可以为您解决一些疑惑，有任何问题欢迎留言反馈，谢谢阅读。