如何高效投放信息流广告以最大化投资回报?
- 行业动态
- 2024-07-30
- 7
信息流广告投放,作为现代网络营销的重要组成部分,是利用互联网平台向潜在消费者传播产品或服务信息的有效手段,小编将}
{概述}={详细解析如何有效地投放信息流广告,以确保广告主能够达到良好的宣传效果及投资回报:
1、选择适当的渠道
了解渠道特性:了解不同渠道的特点和受众群体,抖音、微博、百度、腾讯系和快手等平台都有其独特的用户基础和行为习惯。
匹配产品特性:根据产品特性选择最合适的渠道,视频类、工具类、社交类和资讯类资源适合推广的产品类型各不相同。
2、账户开设与设置
开户流程:选定渠道后,通过代理商或直客开设广告投放账户,这一步骤为后续的广告投放操作提供了基础。
账户操作:账户开立后,广告主需要在账户中设置广告内容,包括定向方式、出价方式等,这些设置将直接影响广告的投放效果。
3、人群分析与定向

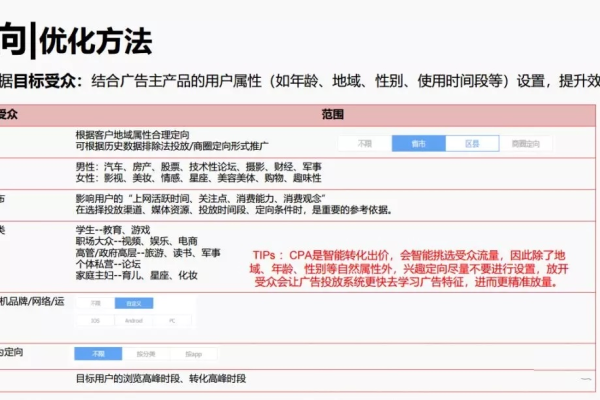
人群画像分析:深入分析目标受众的特征,如年龄、性别、地域和兴趣爱好等,这有助于广告主更精准地定向投放广告。
定向方式确定:结合人群画像和渠道特性,选择合适的定向方式,如基于兴趣的定向、地域定向等,确保广告触达最潜在的客户群体。
4、内容创作与优化
设计高质量内容:制作吸引人的文字、图片、视频等素材,内容需与所选渠道的用户习惯和接受方式相匹配。
A/B测试:尝试不同的广告内容和形式,通过对比测试来找出最佳广告方案,以提高广告的点击率和转化率。
5、数据分析与反馈

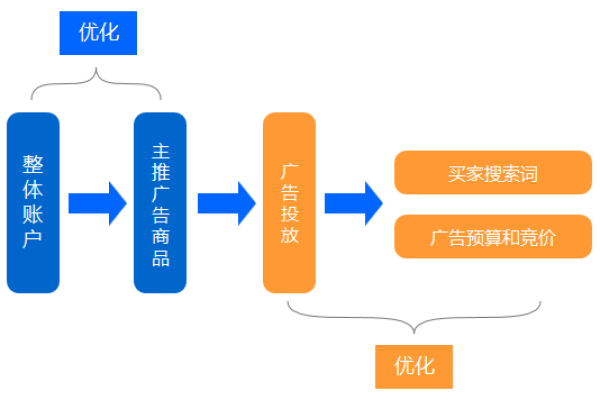
监测广告表现:利用大数据工具监控广告的表现,包括曝光量、点击量、转化率等关键指标。
调整优化策略:根据数据分析的结果,及时调整广告内容、投放时段、预算分配等,以优化广告投放策略。
6、预算与出价策略
合理设定预算:根据广告目标和预期回报,科学设定广告预算,避免因投入不足而影响广告效果,或因过度投入造成资源浪费。
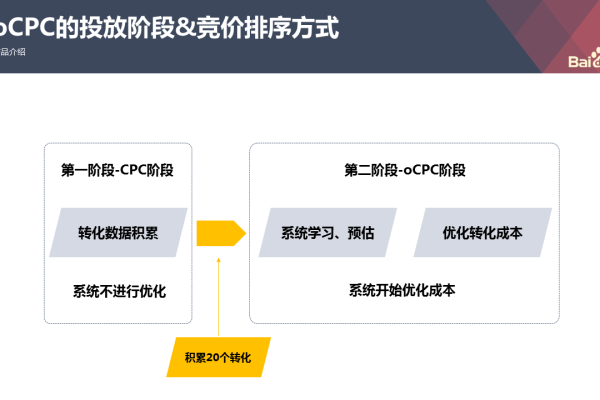
选择出价方式:综合考虑市场竞争和成本效益,选择最合适的出价策略,如CPM(按千次展示计费)、CPC(按点击计费)等。
在上述投放信息流广告的过程中,有几个重要的注意事项需要考虑:

法规遵守:确保广告内容和投放方式符合相关法规和平台政策,避免触犯法律红线。
技术支持:利用先进的技术工具辅助广告投放和效果分析,提高广告投放的精确度和效率。
用户体验:尊重用户体验,避免频繁打扰用户,保持广告与内容的融合度和观赏性。
信息流广告投放是一个系统的过程,涉及到渠道选择、账户管理、人群分析、内容创作、数据监测和策略优化等多个环节,每一步都需要精心设计和执行,以确保广告投放能够达到最佳效果,随着市场环境和技术的发展变化,广告主应持续学习和适应新的广告投放技术和策略,以保持竞争优势。