存储设备冗余_OBS的数据冗余存储方式是什么
- 行业动态
- 2024-06-27
- 6
在当今信息化社会,数据的有效存储和访问变得尤为重要,华为云的对象存储服务(OBS)作为一种可靠的云存储解决方案,提供了不同的数据冗余存储方式以确保数据的持久性和可靠性,使用Erasure Code(EC,即纠删码)算法进行数据冗余是其核心特征之一。
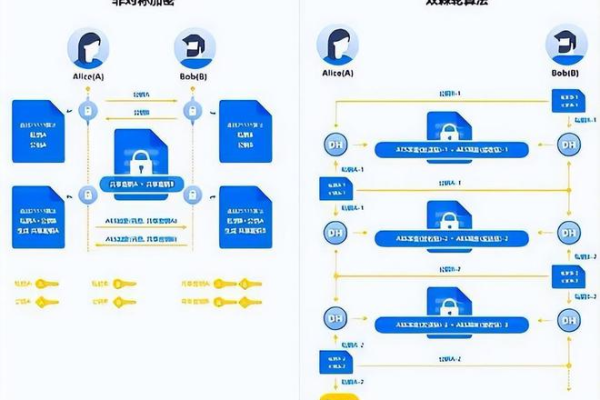
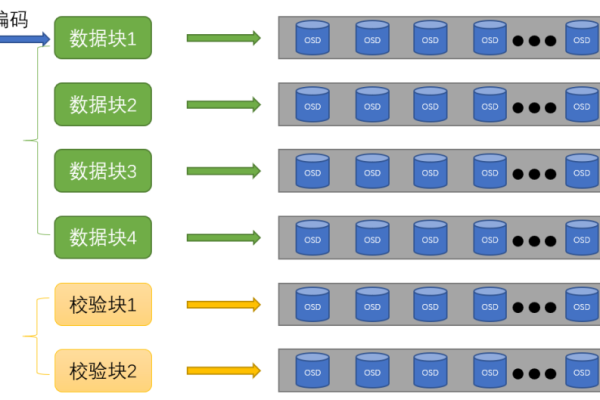
OBS的数据冗余机制主要采用Erasure Code技术,而非传统的多副本方式,在数据存储的过程中,Erasure Code技术通过算法将数据切片并生成校验块,这些校验块和数据切片一起存储,当部分数据发生丢失时,可以利用其他完整的数据和校验块恢复丢失的数据,相比多副本方式,Erasure Code技术可以更高效地利用存储空间,同时还能提供同等级别的数据可靠性保障。
在可用区(AZ)内的节点间,OBS通过应用EC算法来实现数据冗余,对于配置为“单AZ”的桶,它会在该AZ内的多个节点间采用EC算法;而对于配置为“多AZ”的桶,则会在每个AZ内部采用EC算法,同时在不同AZ之间也实现数据复制,从而提升数据耐久性和可用性。
除了数据冗余存储策略之外,OBS还提供了四种不同的存储类别,包括标准存储、低频访问存储、归档存储以及深度归档存储,这些存储类别根据数据的访问模式和存储成本进行了优化,以满足不同业务场景的需求,标准存储针对需要频繁访问的热点文件设计,而低频访问存储则适用于不常访问但仍需快速获取的数据。

进一步地,为了确保关键业务系统的连续性和强一致性,OBS还提供了同城冗余存储类型,该类型能够在极端事件导致某个机房不可用的情况下,仍然保持服务的稳定和可用,这一点对于要求高可用性的业务系统来说至关重要。
华为云OBS通过采用Erasure Code算法实现了高效的数据冗余存储机制,并且结合多种存储类别及同城冗余存储,为客户提供了多样化的数据存储选择,这不仅满足了不同业务场景下对存储性能和成本的需求,还极大地提升了数据的可靠性和持久性。
OBS 数据冗余存储方式的选择依据是什么?
在选择OBS数据冗余存储方式时,主要依据是业务的数据访问模式和容灾需求,如果业务需要频繁访问数据,可以选择标准存储;若数据访问频率不高,可以选择低频访问存储或归档存储以降低成本,同城冗余存储能够为关键业务系统提供更高的数据可用性保障。

OBS 数据冗余存储的安全性如何保证?
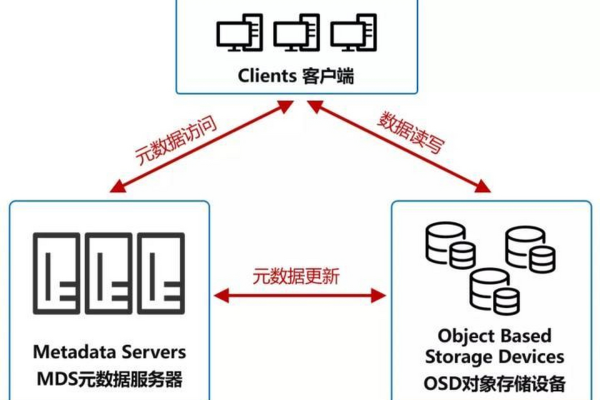
OBS通过在每个可用区内部署多个节点并采用Erasure Code技术,确保了即使部分节点发生故障,数据也能够安全无损地恢复,多AZ配置的桶还能抵御整个数据中心的故障,进一步提高了数据的安全性和可靠性。
以下是关于OBS(对象存储服务,例如阿里云OSS)的数据冗余存储方式的介绍:

| 冗余方式 | 描述 |
| 数据副本 | 在OBS中,用户可以为存储的对象创建多个副本,分布在不同地理位置或数据中心,以实现数据的冗余备份,副本数量可以根据需求进行配置。 |
| 纠删码(EC) | 纠删码是一种数据保护技术,通过将数据分割成多个片段,并为这些片段生成校验码,在OBS中,纠删码可以容忍一定数量的数据丢失或损坏,同时保持数据的完整性和可用性。 |
| 跨区域复制 | 跨区域复制是指将数据在不同区域之间进行复制,以提高数据的可靠性和可用性,在OBS中,用户可以配置跨区域复制规则,实现数据的自动同步。 |
介绍展示了OBS中常见的数据冗余存储方式,包括数据副本、纠删码和跨区域复制,这些方式可以帮助用户实现数据的冗余备份和容错,提高数据的安全性和可靠性。