如何优化dede首页模板以提高SEO排名?
- 行业动态
- 2024-10-01
- 10
在织梦(DedeCMS)内容管理系统中,首页模板的SEO设置至关重要,以下是对dede首页模板的SEO设置的具体介绍:
1、三大标签:系统默认模板的“Title”、“keywords”和“description”标签是直接调用系统后台的设置源,这些标签分别对应网站名称、站点默认关键字和站点描述,虽然“keywords”和“description”标签对SEO的意义可能不如以前那么大,但仍然需要根据具体情况填写,特别是描述性标签,写得好的话能够增加点击率。
2、首页静态化:伪静态对SEO的影响很大,织梦默认模板的配置为域名/index.html的形式,建议统一使用https://www..com/作为首页或标准页,这样有利于优化。
3、修改织梦链:织梦系统自带的链接,即织梦链,是很多SEO不喜欢的,去掉织梦链有两种基本方法:一种是直接在模板中去除相关代码;另一种是在/include/taglib/flinktype.lib.php文件中删除特定代码,需要注意的是,如果系统升级或者覆盖,可能需要重新进行修改。
4、去掉版权链接:建议去掉官方的版权链接,但最好保留部分版权说明,尊重别人的劳动成果,在全站结尾,很多人喜欢使用“次导航”,给一些关键词加个超链,或者加上重点栏目的链接,这也是一个不错的SEO策略。
5、多语言支持:DEDE CMS支持多语言网站,模板也应提供相应的语言文件夹和语言切换功能。
6、自定义字段:DEDE内容页可以调用自定义字段来设置SEO标题、描述和关键字,这对于提升网站在搜索引擎中的排名非常有帮助。
7、注意事项:在修改任何代码之前,务必备份原始文件,以防万一出现问题时能够恢复。
通过上述设置,可以有效地提升网站的SEO效果,吸引更多的流量和用户,希望这些信息对你有所帮助!
dede首页模板的SEO设置是确保网站在搜索引擎中获取良好排名的关键步骤,以下是一些专业、准确且具有见地的SEO设置建议,适用于使用织梦(dede)系统的网站:
1、标题(Title)设置:
确保首页标题包含核心关键词,并反映网站的主要内容和价值。
标题长度一般控制在5060个字符以内,避免过长影响用户体验。
2、关键词(Keywords)设置:
在首页的关键词标签中,列出与网站内容最相关的35个关键词。

关键词应与标题一致,且在内容中自然分布。
3、描述(Description)设置:
描述标签应简要网站的主要内容,包含关键词,长度在150200个字符左右。
描述要吸引人,激发用户点击的欲望。
4、URL优化:
使用友好的URL结构,如“/category/productid.html”而不是“/index.php?c=product&id=123”。
确保URL中包含关键词,便于搜索引擎抓取。
5、HTML标签优化:
使用<h1>标签来强调首页的标题,如果可能,确保标题中包含关键词。
使用适当的<h2>、<h3>等标签来组织内容,提高内容的层次结构。
6、图片优化:

为首页的图片添加alt属性,包含关键词描述图片内容。
确保图片文件名简洁,包含关键词。
7、内部链接:
在首页合理布局内部链接,引导用户访问网站其他页面。
使用锚文本(锚点文本)链接,包含关键词。
8、移动端优化:
确保网站响应式设计,适应不同设备屏幕。
移动端页面也应进行SEO优化。
9、加载速度优化:
优化图片和视频等媒体文件,减小文件大小。
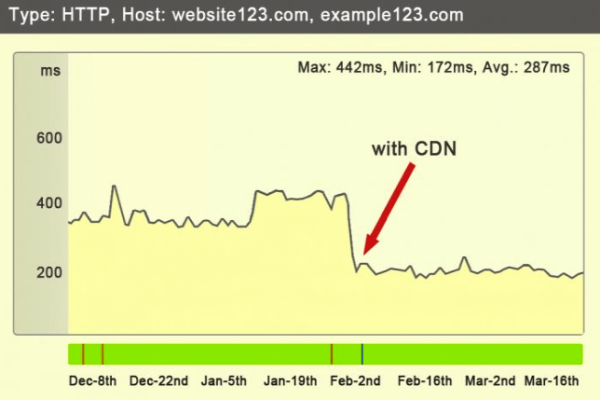
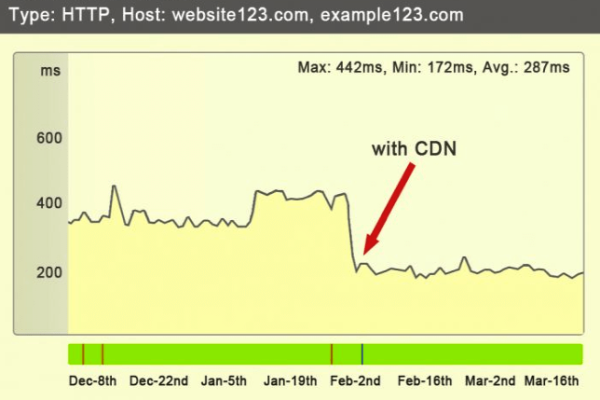
使用CDN(内容分发网络)提高加载速度。

10、社交媒体集成:
在首页集成社交媒体分享按钮,鼓励用户分享内容。
确保社交媒体链接的SEO优化。
11、元标签和头部标签:
使用元标签如robots.txt来指导搜索引擎的爬虫行为。
使用rel=canonical防止重复内容。
12、内容质量:
确保首页内容丰富、有价值,定期更新。
提供独特的、有吸引力的内容,以吸引用户和搜索引擎。
通过以上这些SEO设置,可以有效提升dede首页模板的搜索引擎优化效果,从而提高网站在搜索引擎中的排名和可见度。