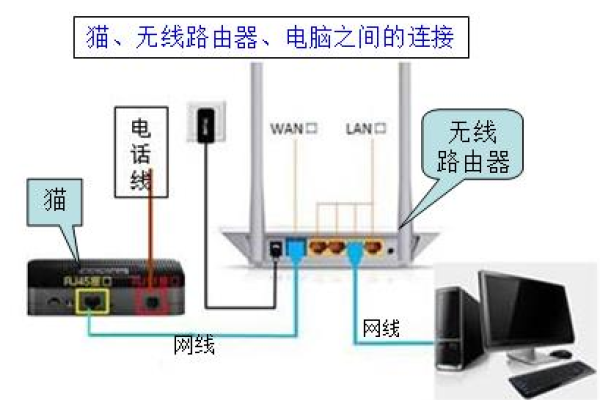
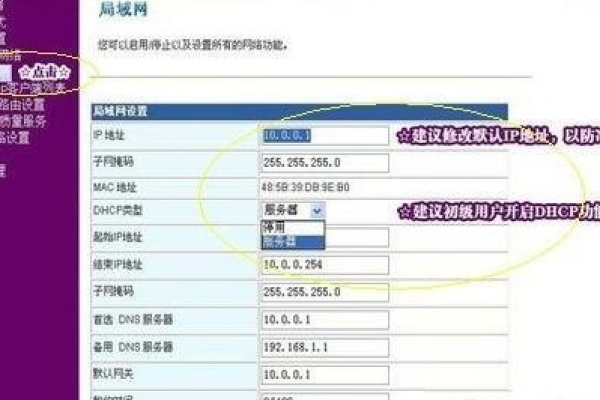
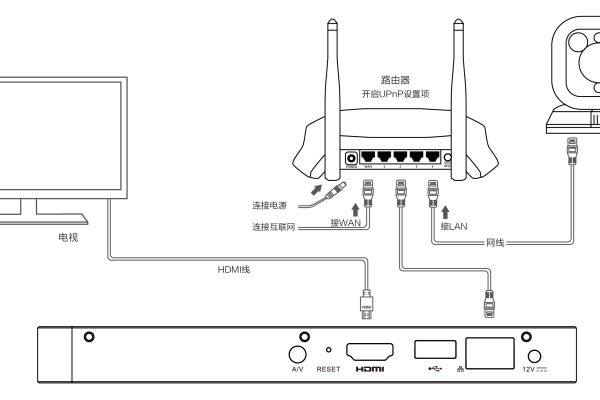
思科路由器 视频设置教程
- 行业动态
- 2024-02-22
- 10
本教程将指导您如何设置思科路由器的视频功能,包括连接设备、配置网络设置等步骤。
思科路由器视频
思科路由器是全球领先的网络设备供应商,其产品广泛应用于各种规模的企业、政府和教育机构,在这篇文章中,我们将详细介绍思科路由器的工作原理、功能特点以及如何配置和使用思科路由器。
思科路由器的工作原理
1、数据包转发
思科路由器的核心功能是数据包转发,当数据包从一个网络接口进入路由器时,路由器会根据目的IP地址查找路由表,然后将数据包从适当的出口接口转发出去,这个过程通常非常快速,因为路由器使用硬件实现高速转发。
2、路由协议
思科路由器支持多种路由协议,如RIP、OSPF、EIGRP等,这些协议允许路由器之间交换路由信息,以便它们可以构建和维护精确的路由表,路由协议的选择取决于网络的规模、拓扑结构和性能要求。
3、安全特性
思科路由器提供了许多安全特性,以保护网络免受未经授权的访问和攻击,这些特性包括访问控制列表(ACL)、防火墙、网络传输层等,通过配置这些安全特性,管理员可以确保网络的安全和稳定运行。
思科路由器的功能特点
1、高性能
思科路由器采用高性能的处理器和大容量的内存,可以实现高速的数据包转发和复杂的路由计算,这使得思科路由器非常适合处理大型企业和数据中心的大量流量。
2、高可靠性

思科路由器具有高可靠性,可以在各种恶劣环境下稳定运行,思科还提供了丰富的故障诊断和恢复工具,帮助管理员快速解决网络问题。
3、强大的扩展性
思科路由器支持模块化设计,可以根据网络需求灵活扩展各种接口和服务,这使得思科路由器可以轻松应对不断变化的网络环境。
4、丰富的管理功能
思科路由器提供了丰富的管理功能,包括命令行界面(CLI)、图形用户界面(GUI)和远程管理等,这些功能使得管理员可以轻松地配置和管理路由器。
如何配置和使用思科路由器
1、连接路由器
将计算机连接到路由器的管理接口(通常是串口或以太网口),使用终端仿真软件(如SecureCRT或PuTTY)建立与路由器的连接。
2、进入特权模式

在连接成功后,输入“enable”命令进入特权模式,在特权模式下,可以执行全局配置命令。
3、配置路由协议
根据网络的需求,选择合适的路由协议并配置相应的参数,如果使用RIP协议,需要配置网络号、版本号等参数。
4、配置接口和安全特性
为路由器的各个接口分配IP地址和子网掩码,并配置相应的安全特性(如ACL、防火墙等)。
5、保存配置并退出
在完成所有配置后,输入“write memory”命令保存配置,输入“exit”命令退出特权模式。
相关问题与解答
1、问题:思科路由器支持哪些路由协议?

答:思科路由器支持多种路由协议,如RIP、OSPF、EIGRP等,具体支持哪些协议取决于路由器的型号和软件版本。
2、问题:如何查看思科路由器的配置?
答:可以使用终端仿真软件(如SecureCRT或PuTTY)连接到路由器的管理接口,然后输入“show running-config”命令查看当前配置。
3、问题:如何备份思科路由器的配置?
答:在特权模式下,输入“copy running-config startup-config”命令可以将当前配置保存到启动配置文件中,这样,即使重启路由器,配置也不会丢失。
4、问题:如何升级思科路由器的软件?
答:连接到路由器的管理接口并进入特权模式,输入“copy startup-config running-config”命令备份当前配置,接下来,使用TFTP服务器将新的软件映像文件上传到路由器,输入“reload”命令重启路由器并应用新软件。