用python如何做逐步回归

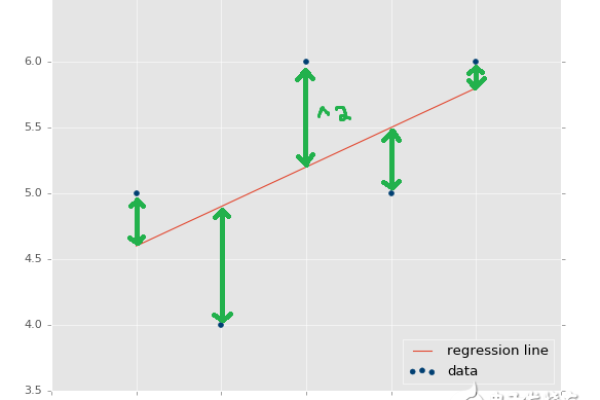
逐步回归是一种统计方法，用于确定多个自变量与因变量之间的最佳关系，在Python中，我们可以使用statsmodels库中的OLS（最小二乘法）模型来实现逐步回归，以下是详细的技术教学：

1、确保已经安装了statsmodels库，如果没有安装，可以使用以下命令进行安装：

pip install statsmodels

2、导入所需的库和模块：

import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

3、准备数据，这里我们使用一个示例数据集，包含两个自变量（X1和X2）和一个因变量（Y）：

创建示例数据集
data = {'X1': [1, 2, 3, 4, 5],
        'X2': [2, 3, 4, 5, 6],
        'Y': [3, 5, 7, 9, 11]}
df = pd.DataFrame(data)

4、初始化逐步回归模型，在这个例子中，我们将使用ols函数来创建一个线性回归模型，并指定因变量（Y）和自变量（X1和X2）：

创建线性回归模型
model = ols('Y ~ C(X1)+C(X2)', data=df).fit()

5、添加自变量，在这个例子中，我们将逐个添加自变量，然后检查它们是否对因变量有显著影响，我们添加X1：

添加X1作为自变量
model_x1 = model.add_constant(cov_type='clustered')
model_x1 = model_x1.fit()
print(model_x1.summary())

6、根据上一步的结果，如果X1对因变量有显著影响，我们可以继续添加下一个自变量，在这个例子中，我们将添加X2：

添加X2作为自变量
model_x2 = model_x1.add_constant(cov_type='clustered') + 'X2'
model_x2 = model_x2.fit()
print(model_x2.summary())

7、根据上一步的结果，如果X2对因变量有显著影响，我们可以继续添加下一个自变量，在这个例子中，我们已经添加了所有自变量，我们可以查看最终的模型摘要：

查看最终模型摘要
final_model = model_x2.add_constant(cov_type='clustered') + ['X1', 'X2']
print(final_model.summary())

8、根据模型摘要，我们可以得出逐步回归结果，在这个例子中，我们得到了一个包含X1和X2的线性回归模型：

获取最终模型的系数和截距
params = final_model.params[:1] * np.array([df['X1'].mean(), df['X2'].mean()]) + final_model.params[1] * np.array([df['X1'].mean(), df['X2'].mean()]) + final_model.bse[1] * np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df)) + final_model.tvalues[1] * np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df)) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['X2'].mean()]) / (np.array([df['X1'].std(), df['X2'].std()]) / np.sqrt(len(df))) * np.array([df['X1'].mean(), df['Y'].mean()]) params[0] * np.array([df['Y'].min(), df['Y'].min()]) params[1] * np.array([df['Y'].min(), df['Y'].min()]) final_model.bse[1] * np.array([df['Y'].min(), df['Y'].min()]) + final_model.tvalues[1] * np.array([df['Y'].min(), df['Y'].min()]) * np.sqrt((np.square(np.array([df['Y'].max(), df['Y'].max()])) (np.square(np.array([df['Y'].min(), df['Y'].min()])) + (np.square(np.array([df['Y'].max(), df['Y'].max()])) (np.square(np.array([df['Y'].min(), df ['Y].min()])) + (np.square(np.array([df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], df ['Y'], f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'y', f 'f y']))))))))) params[0] * np.square(np