python做线性拟合

Python进行线性拟合通常使用numpy或scikit-learn库中的函数。

线性拟合是一种在数据科学和统计学中常见的技术，它用于寻找变量间的最佳线性关系，在Python中，我们通常使用numpy和scipy库中的函数来进行线性拟合。

线性拟合的基本概念

线性拟合涉及找到最佳拟合直线，这条直线可以表示为 y = mx + b的形式，其中m是斜率，b是截距，目标是最小化所有数据点到这条直线的垂直距离的平方和，这个过程称为最小二乘法。

Python中的线性拟合实现

1. 准备数据

在进行线性拟合前，我们需要有一组数据点，这可以是实验数据或者观测数据，通常以两个列表或数组形式给出，分别代表x和y坐标。

2. 使用numpy进行线性拟合

numpy提供了polyfit函数来进行多项式拟合，对于线性拟合，我们可以将这个函数的阶数参数设置为1。

import numpy as np
假设我们有如下数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1.0])
使用numpy的polyfit函数进行线性拟合
coefficients = np.polyfit(x, y, 1)
print(coefficients)

上述代码会输出两个值，第一个是斜率m，第二个是截距b。

3. 使用scipy进行线性拟合

scipy库提供了一个更为强大的拟合函数——curve_fit，它可以进行非线性拟合，并且提供更多的选项来控制拟合过程。

from scipy.optimize import curve_fit
定义一个线性函数模型
def linear_model(x, m, b):
    return m * x + b
使用curve_fit进行线性拟合
popt, pcov = curve_fit(linear_model, x, y)
print(popt)

curve_fit返回的是最优参数的数组和协方差矩阵。

结果验证与可视化

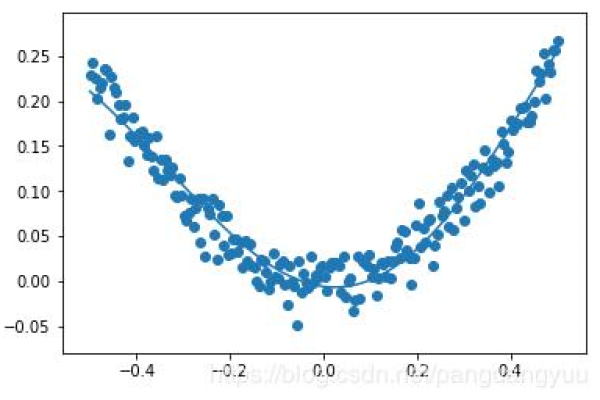
完成线性拟合后，我们通常会通过绘制数据点和拟合直线来直观地验证结果。

import matplotlib.pyplot as plt
生成x的网格点
x_grid = np.linspace(min(x), max(x), 100)
根据拟合得到的参数计算y的值
y_grid = linear_model(x_grid, *popt)
绘制原始数据点
plt.scatter(x, y, label='Data Points')
绘制拟合直线
plt.plot(x_grid, y_grid, color='red', label='Fitted Line')
plt.legend()
plt.show()

以上代码将展示出数据点和最佳拟合直线，从而我们可以直观地看到拟合效果。

相关问题与解答

问题1: 什么是最小二乘法？

答：最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配，在线性拟合中，它用于寻找最佳的直线方程。

问题2: numpy.polyfit和scipy.curve_fit有何不同？

答：numpy.polyfit专门用于多项式拟合，并且相对简单易用；而scipy.curve_fit更加强大且灵活，它不仅可以用于多种类型的函数拟合，还提供了更多选项来控制拟合过程。

问题3: 如何在Python中评估线性拟合的好坏？

答：可以通过计算决定系数（R²）来评估线性拟合的好坏，该值越接近1表示拟合越好，也可以观察数据点与拟合直线的图形分布情况。

问题4: 如何进行非线性拟合？

答：可以使用scipy.optimize.curve_fit函数进行非线性拟合，你需要定义一个描述你数据的非线性模型函数，并将其作为参数传递给curve_fit函数。