jquery上下自动轮播代码怎么写
- 行业动态
- 2024-03-23
- 3
jQuery是一个快速、简洁的JavaScript库,它可以简化HTML文档遍历、事件处理、动画设计和Ajax交互等操作,在网页开发中,我们经常需要实现一些动态效果,如轮播图、下拉菜单等,本文将详细介绍如何使用jQuery实现上下自动轮播的效果。
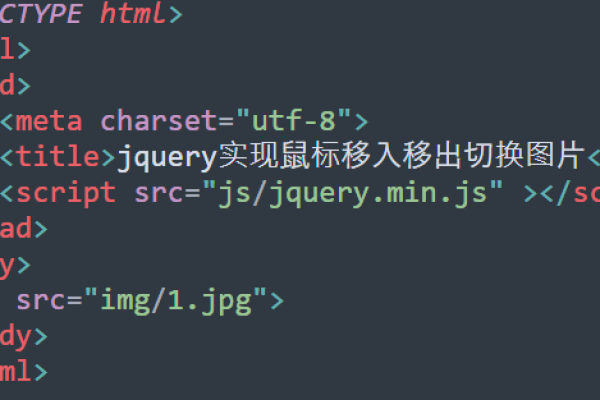
我们需要引入jQuery库,在HTML文件中添加以下代码:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF8">
<meta name="viewport" content="width=devicewidth, initialscale=1.0">
<title>jQuery轮播图</title>
<script src="https://code.jquery.com/jquery3.6.0.min.js"></script>
</head>
<body>
<!在这里编写轮播图的HTML结构 >
</body>
</html>
接下来,我们编写轮播图的HTML结构,在<body>标签内添加以下代码:

<div class="slider">
<ul class="slides">
<li><img src="image1.jpg" alt="图片1"></li>
<li><img src="image2.jpg" alt="图片2"></li>
<li><img src="image3.jpg" alt="图片3"></li>
<!更多图片 >
</ul>
</div>
在这个例子中,我们创建了一个名为.slider的容器,用于包裹轮播图的所有内容,在.slider内部,我们创建了一个名为.slides的无序列表,用于存放所有的图片,每个图片项都是一个<li>标签,包含一个<img>标签,用于显示图片,你可以根据需要添加更多的图片。
接下来,我们编写CSS样式,在<head>标签内添加以下代码:

<style>
.slider {
width: 100%;
height: 300px;
overflow: hidden;
position: relative;
}
.slides {
liststyle: none;
margin: 0;
padding: 0;
position: absolute;
top: 0;
left: 0;
}
.slides li {
float: left;
width: 100%;
height: 300px;
backgroundsize: cover;
backgroundposition: center;
backgroundrepeat: norepeat;
}
</style>
在这个例子中,我们设置了轮播图的宽度和高度,并隐藏了溢出的内容,我们将.slides设置为绝对定位,使其相对于.slider进行定位,我们设置了图片列表的样式,使图片浮动并占据整个容器宽度,我们还设置了背景图片的大小、位置和重复方式,你可以根据需要调整这些样式。
现在,我们可以编写jQuery代码来实现轮播效果,在<script>标签内添加以下代码:

$(document).ready(function() {
let currentIndex = 0; // 当前显示的图片索引
let slides = $(".slides"); // 获取图片列表元素
let slideCount = slides.children().length; // 获取图片数量
let slideWidth = slides.width(); // 获取每张图片的宽度
let interval = 3000; // 设置轮播间隔时间(毫秒)
let autoPlay = true; // 是否自动播放轮播图
// 初始化轮播图位置和透明度
slides.css({left: slideWidth}); // 将第一张图片移到最左侧
slides.children().first().fadeIn(100); // 显示第一张图片,其他图片隐藏
slides.children().not(":first").hide(); // 隐藏除第一张图片外的其他图片
// 监听鼠标悬停事件,暂停自动播放和切换按钮的显示/隐藏状态
$(".slider").hover(function() {
autoPlay = false; // 暂停自动播放轮播图
$(this).find(".pause, .play").show(); // 显示暂停和播放按钮
}, function() {
autoPlay = true; // 恢复自动播放轮播图
$(this).find(".pause, .play").hide(); // 隐藏暂停和播放按钮
});
// 监听点击暂停按钮事件,暂停或恢复自动播放轮播图,并切换按钮的显示/隐藏状态
$(".pause").click(function() {
if (autoPlay) {
autoPlay = false; // 暂停自动播放轮播图
$(this).text("继续播放"); // 修改按钮文本为“继续播放”
} else {
autoPlay = true; // 恢复自动播放轮播图
$(this).text("暂停播放"); // 修改按钮文本为“暂停播放”
}
});
});
在这个例子中,我们首先定义了一些变量,如当前显示的图片索引、图片列表元素、图片数量、每张图片的宽度、轮播间隔时间和是否自动播放轮播图,我们初始化了轮播图的位置和透明度,并将第一张图片移到最左侧,接着,我们监听了鼠标悬停事件,暂停自动播放和切换按钮的显示/隐藏状态,我们监听了点击暂停按钮事件,暂停或恢复自动播放轮播图,并切换按钮的显示/隐藏状态。