平台短信接口_开放平台接口
- 行业动态
- 2024-07-07
- 4
平台短信接口与开放平台接口
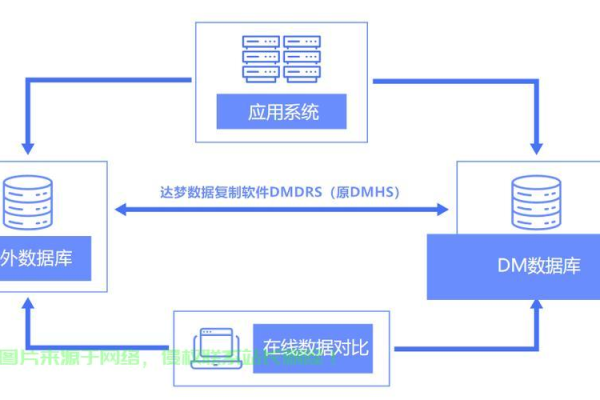
在数字化时代,企业与用户之间的沟通越来越依赖于快速、高效的信息传递方式,平台短信接口和开放平台接口是实现这一目标的关键技术手段,本文将详细介绍这两种接口的功能、使用方法以及它们如何帮助企业提升服务质量和效率。
平台短信接口
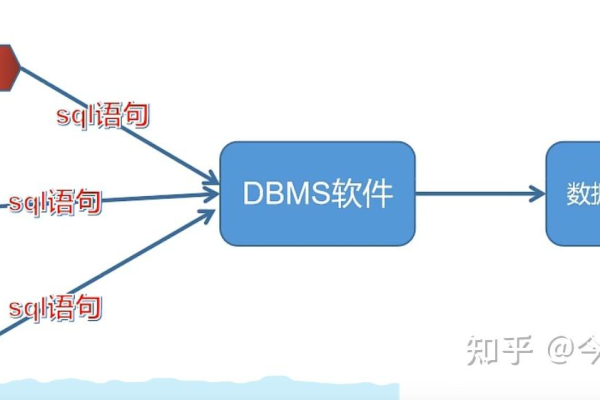
平台短信接口是指允许软件应用通过编程方式发送短信到用户手机的一种服务接口,这种接口通常由专业的通信服务提供商提供,它们拥有与移动网络运营商直连的短信发送能力。
功能特点
即时性: 短信发送几乎是实时的,确保信息能够快速到达接收者。
覆盖广: 可覆盖不同运营商的用户,实现跨网络的信息传递。
集成易: 提供API接口,易于集成到各种软件平台和应用中。
成本低: 相比其他通讯方式,短信具有较低的成本。
自动化: 支持触发式发送,例如事务验证、预警通知等。
应用场景
用户注册验证
交易安全确认
营销活动通知
客户服务提醒
紧急信息发布
使用方法
1、选择提供商: 根据价格、服务质量、技术支持等因素选择合适的短信服务提供商。
2、注册账户: 在提供商处注册账户并获取API访问权限和密钥。
3、集成API: 按照提供商的文档将API集成到您的应用中。
4、测试发送: 进行测试以确保短信发送功能正常。

5、监控反馈: 利用提供商的监控工具跟踪短信发送状态和用户反馈。
开放平台接口
开放平台接口是指由软件或服务的提供方公开的一系列接口,允许第三方开发者访问平台资源,如数据、计算能力或其他服务,以创建新的应用或扩展现有应用的功能。
功能特点
扩展性: 允许第三方服务接入,扩展平台功能。
标准化: 遵循一定的标准和协议,保证不同系统间的兼容性。
安全性: 提供认证和授权机制,保护数据安全。
多样性: 支持多种类型的服务接口,如RESTful API、SOAP等。
应用场景
社交媒体集成
支付系统集成
数据共享与分析
多平台同步操作
定制化服务开发
使用方法
1、了解平台政策: 阅读平台的开发者文档和服务条款。
2、注册开发者账号: 在平台上注册账号并获得API访问权限。
3、获取API密钥: 申请API密钥以便进行身份验证。
4、接口调用: 根据文档使用API进行数据请求和处理。
5、开发与测试: 开发应用并进行充分的测试以确保稳定性和性能。
6、部署上线: 将应用部署到生产环境并监控其运行状况。
结合使用的优势
将平台短信接口与开放平台接口结合使用,可以带来以下优势:
增强用户体验: 通过开放平台接口获取用户行为数据,然后利用短信接口发送个性化通知,提高用户满意度。
提升效率: 自动化处理流程,减少人工干预,提高工作效率。
扩大影响力: 利用开放平台的资源和数据,通过短信接口快速传播信息,扩大品牌影响力。
表格归纳
| 类型 | 功能特点 | 应用场景 | 使用方法步骤 |
| 短信接口 | 即时性、覆盖广、集成易、成本低、自动化 | 用户验证、交易确认、营销通知、服务提醒、紧急信息发布 | 选择提供商 → 注册账户 → 集成API → 测试发送 → 监控反馈 |
| 开放平台接口 | 扩展性、标准化、安全性、多样性 | 社交集成、支付集成、数据共享、多平台操作、定制服务开发 | 了解政策 → 注册账号 → 获取密钥 → 接口调用 → 开发测试 → 部署上线 |
相关问答FAQs
Q1: 如何确保短信接口的安全性?
A1: 确保短信接口的安全性需要采取以下措施:
加密传输: 使用HTTPS或其他加密协议来保护数据在传输过程中的安全。
API密钥管理: 妥善保管API密钥,避免泄露,并定期更换密钥。
限制访问: 设置IP白名单,只允许特定IP地址访问API。
防止滥用: 实施速率限制和验证措施,防止反面攻击和滥用。
监控与响应: 监控短信发送行为,对于异常行为要及时响应和处理。
Q2: 开放平台接口的数据格式有哪些?
A2: 开放平台接口常见的数据格式包括:
JSON: 轻量级的数据交换格式,易于人阅读和编写,同时也易于机器解析和生成。
XML: 一种标记语言,用于编码文档和数据,具有高度的可扩展性和灵活性。
CSV: 逗号分隔值格式,通常用于表格数据的表示和交换。
YAML: 专门用于数据序列化的简洁高效的格式。
Form Encoded: 主要用于HTTP请求体中的数据提交,数据以键值对的形式表示。