BP神经网络的收敛性,关键因素与优化策略有哪些?
- 行业动态
- 2024-11-19
- 3065
BP神经网络的收敛条件主要包括学习率、动量因子、激活函数等的选择和调整。学习率控制权重更新步长,过大可能导致不稳定,过小则收敛缓慢。动量因子用于平滑权值更新,防止陷入局部极小值。非线性激活函数引入非线性,使网络能学习复杂关系。
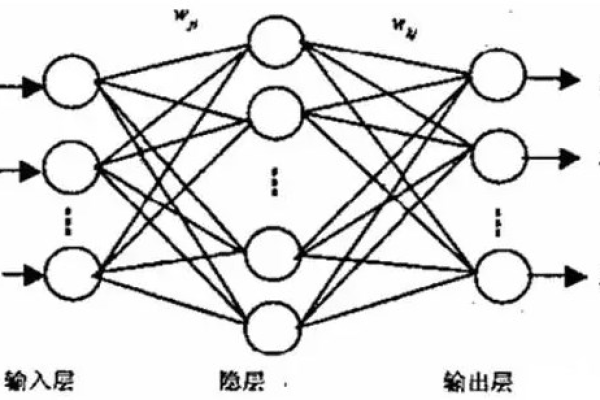
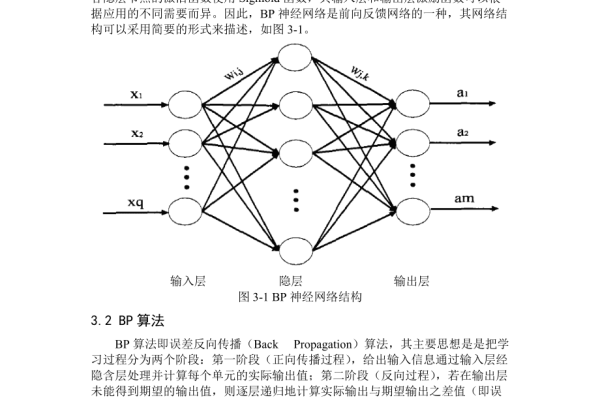
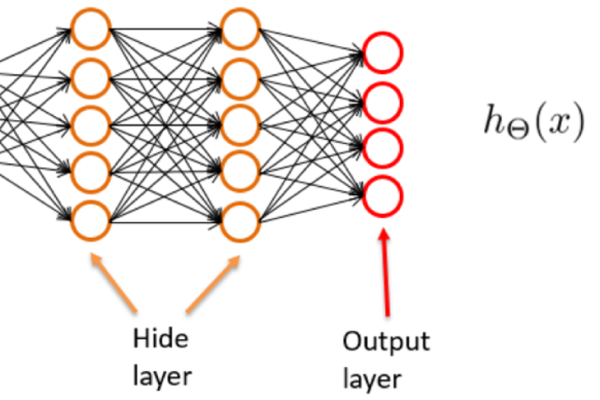
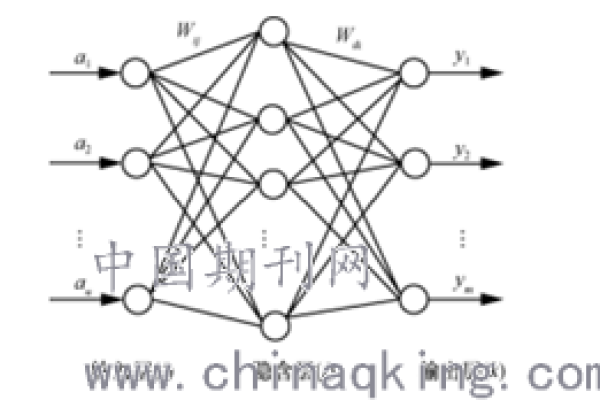
BP神经网络,即反向传播神经网络,是一种多层前馈神经网络,因其在解决复杂非线性问题中的有效性而闻名,BP神经网络由输入层、隐含层和输出层组成,其中隐含层可以有多个,其工作原理是通过误差反向传播算法来调整网络权重,以最小化损失函数。
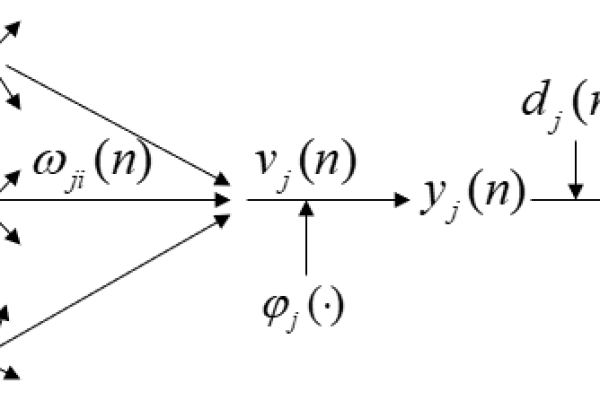
一、BP神经网络的收敛条件
1. 学习率(α)
定义:学习率是控制权值更新的步长,它决定了每次权重调整的幅度。
影响:较大的学习率可能导致网络不稳定,甚至发散;较小的学习率则可能导致收敛速度缓慢,但能更稳定地接近全局最优解。
2. 动量因子(β)
定义:动量因子用于平滑权值更新,帮助网络跳出局部极小值。
作用:通过加入前一次权重更新的一部分到本次更新中,动量因子能够加速收敛并减少震荡。
3. 激活函数
类型:常用的激活函数包括Sigmoid、ReLU等,它们引入非线性,使网络能够学习复杂关系。
选择:不同的激活函数对网络的训练效果和收敛速度有显著影响,ReLU激活函数相比Sigmoid在深层网络中更能缓解梯度消失问题。
二、BP神经网络的收敛性证明
1. 梯度下降法
原理:BP神经网络使用梯度下降法来最小化损失函数,梯度下降法通过计算损失函数关于权值的负梯度,并沿着该方向更新权值,逐步逼近局部极小值。
过程:在每次迭代中,网络根据当前的权值计算损失函数的梯度,然后按照学习率调整权值,使损失函数逐渐减小。
2. 误差反向传播算法
步骤:首先进行前向传播,计算网络的输出与期望输出之间的误差;然后进行反向传播,将误差从输出层向输入层逐层传播,并根据误差计算各层的灵敏度(即损失函数关于权值的导数);最后根据灵敏度和学习率更新权值。
效果:通过不断迭代前向传播和反向传播过程,网络的权值逐渐调整到使损失函数最小化的状态,从而实现收敛。
三、训练数据集选择
1. 代表性
要求:训练数据集应充分代表问题域,包含各种可能遇到的输入和输出模式。
目的:确保网络能够学习到问题的内在规律,提高泛化能力。
2. 多样性
要求:训练数据集应具有多样性,避免出现重复或相似的样本。
作用:防止网络过拟合,提高网络对新数据的适应能力。
3. 无噪声
要求:训练数据集应尽量无噪声,避免引入不必要的干扰。
方法:可以通过数据清洗、去噪等方法提高数据质量。
四、网络结构设计
1. 层数和节点数
层数:增加层数可以提高网络的表达能力,但也会增加计算复杂度和训练时间。
节点数:每层的节点数也会影响网络的性能和收敛速度,需要根据具体问题进行调整。
2. 初始化权值和偏置
重要性:合理的初始化有助于加快收敛速度和避免陷入局部极小值。
方法:通常采用随机初始化或He初始化等方法。
五、FAQs
Q1: 为什么BP神经网络容易陷入局部极小值?
A1: BP神经网络采用梯度下降法进行优化,而梯度下降法只能保证收敛到局部极小值而非全局最优解,损失函数的非凸性以及初始化权值和偏置的随机性也可能导致网络陷入局部极小值,为了缓解这一问题,可以采用动量法、学习率衰减、正则化等技术手段来帮助网络跳出局部极小值。
Q2: 如何选择合适的学习率和动量因子?
A2: 选择合适的学习率和动量因子是BP神经网络训练中的关键步骤之一,学习率过大可能导致网络发散或不稳定;学习率过小则会导致收敛速度缓慢,动量因子的取值也需要根据具体问题进行调整以平衡收敛速度和稳定性,通常可以通过实验或交叉验证的方法来确定最佳的学习率和动量因子组合,此外还可以采用自适应学习率算法(如Adam)来动态调整学习率以加速收敛过程。
以上内容就是解答有关“bp神经网络 收敛条件”的详细内容了,我相信这篇文章可以为您解决一些疑惑,有任何问题欢迎留言反馈,谢谢阅读。
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/251148.html