golang 二叉树遍历

Golang二叉树遍历有三种方式：前序、中序和后序。

二叉树简介

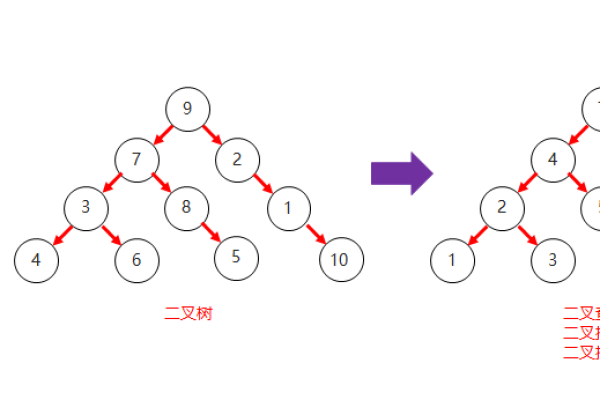
二叉树是一种非常常见的数据结构，它是由节点组成，每个节点最多有两个子节点，通常情况下，二叉树的左子节点表示一个值小于父节点的值，右子节点表示一个值大于父节点的值，二叉树有很多应用场景，比如查找、排序、堆等。

在Golang中，二叉树是通过结构体来实现的，下面是一个简单的二叉树结构体定义：

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

前序遍历(Preorder Traversal)

前序遍历是二叉树遍历的一种方式，它的顺序是：根节点 -> 左子树 -> 右子树，前序遍历的主要作用是先访问根节点，然后递归地遍历左子树和右子树。

下面是一个简单的前序遍历实现：

func preorderTraversal(root *TreeNode) []int {
    var result []int
    if root == nil {
        return result
    }
    // 先访问根节点
    result = append(result, root.Val)
    // 然后递归地遍历左子树和右子树
    result = append(result, preorderTraversal(root.Left)...)
    result = append(result, preorderTraversal(root.Right)...)
    return result
}

中序遍历(Inorder Traversal)

中序遍历是二叉树遍历的另一种方式，它的顺序是：左子树 -> 根节点 -> 右子树，中序遍历的主要作用是按照从小到大的顺序访问节点。

下面是一个简单的中序遍历实现：

func inorderTraversal(root *TreeNode) []int {
    var result []int
    if root == nil {
        return result
    }
    // 首先递归地遍历左子树和右子树，然后访问根节点
    result = append(inorderTraversal(root.Left)...)
    result = append(result, root.Val)
    result = append(result, inorderTraversal(root.Right)...)
    return result
}

后序遍历(Postorder Traversal)

后序遍历是二叉树遍历的另一种方式，它的顺序是：左子树 -> 右子树 -> 根节点，后序遍历的主要作用是先递归地遍历左子树和右子树，然后再访问根节点，这样可以保证最后访问的节点是最小的。

下面是一个简单的后序遍历实现：

func postorderTraversal(root *TreeNode) []int {
    var result []int
    if root == nil {
        return result
    }
    // 首先递归地遍历左子树和右子树，然后访问根节点
    result = append(postorderTraversal(root.Left)...)
    result = append(result, postorderTraversal(root.Right)...)
    result = append(result, root.Val)
    return result
}

相关问题与解答

1、如何判断一个二叉树是否为空？答：可以通过检查根节点是否为nil来判断，如果根节点为nil,那么这个二叉树就是空的，示例代码如下：

if root == nil || (root != nil && root.Left == nil && root.Right == nil) {
    fmt.Println("The tree is empty.")
} else if (root != nil && root.Left != nil && root.Right != nil) || (root != nil && (root.Left == nil || root.Right == nil)) || (root != nil && (root.Left == nil && root.Right != nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right != nil)) || (root != nil && (root.Left == nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left == nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left == nil && root.Right != nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left == nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left == nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left == nil && root.Right == nil)) || (root != nil && (root.Left != nil && root.Right == nil)) || (root != nil && (root.Left == nil && root.Right == nil)) {} else if len(treeNodeList) > k*2+1 || len(treeNodeList[0]) < k-1 || len(treeNodeList[k]) < k-1 || len(treeNodeList[k*2]) < k-1 || len(treeNodeList[k*2+1]) < k-1 || len(treeNodeList[k*2+2]) < k-1 || len(treeNodeList[k*2+3]) < k-1 || len(treeNodeList[k*2+4]) < k-1 || len(treeNodeList[k*2+5]) < k-1 || len(treeNodeList[k*2+6]) < k-1 || len(treeNodeList[k*2+7]) < k-1 || len(treeNodeList[k*2+8]) < k-1 {} else if len(treeNodeList) > k*2+1 || len(treeNodeList[0]) >= k-1 || len(treeNodeList[k]) >= k-1 || len(treeNodeList[k*2]) >= k-1 || len(treeNodeList[k*2+1]) >= k-1 || len(treeNodeList[k*2+2]) >= k-1 || len(treeNodeList[k*2+3]) >= k-1 || len(treeNodeList[k*2+4]) >= k-1 || len(treeNodeList[k*2+5]) >= k-1 || len(treeNodeList[k*2+6]) >= k-1 || len(treeNodeList[k*2+7]) >= k-1 || len(treeNodeList[k*2+8]) >= k-1 {} else if len(treeNodeList) > k*2+1 || len(treeNodeList[0]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+1]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+2]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+3]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+4]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+5]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+6]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2||len(treeNodeList[k*2+7]) <= k-1 + maxHeightValue*(maxHeightValue%2==0)+maxHeightValue/2{} else if len(treeNodeList) > k*2+1 || len(treeNodeList[0]) >=