如何设计一个高效的大型分布式网站架构?
- 行业动态
- 2024-08-01
- 11
【大型分布式网站架构】
大型分布式网站架构旨在处理众多用户访问,提供高流量和高并发的服务环境,这类架构需要具备高性能、高可用性、可伸缩性、安全性以及扩展性,在设计时,还需考虑渐进发展和以用户为中心的原则,确保服务从小规模逐渐扩展到能支撑海量数据和复杂功能的大型系统。
【核心特点与目标】
大型分布式网站的基础特征包括面向广泛且分布的用户群体、处理大规模数据流、维护高服务水平、抵御网络攻击以及频繁的功能更新和发布,这些特性决定了网站架构必须致力于实现一系列目标:快速响应的高性能,持续稳定的高可用性,灵活调节资源以应对需求变化的可伸缩性,保护数据和用户隐私的安全性,以及能够适应新功能模块添加的扩展性。
【架构模式与技术选型】
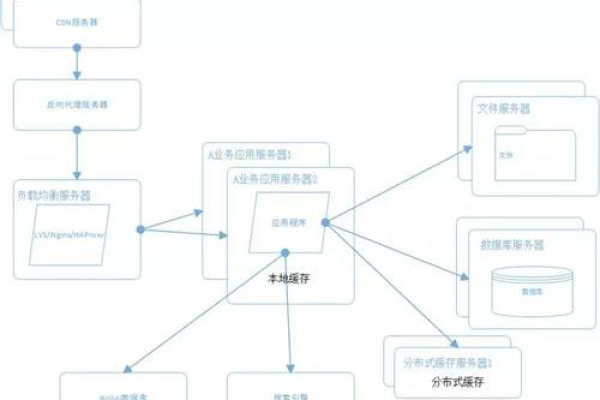
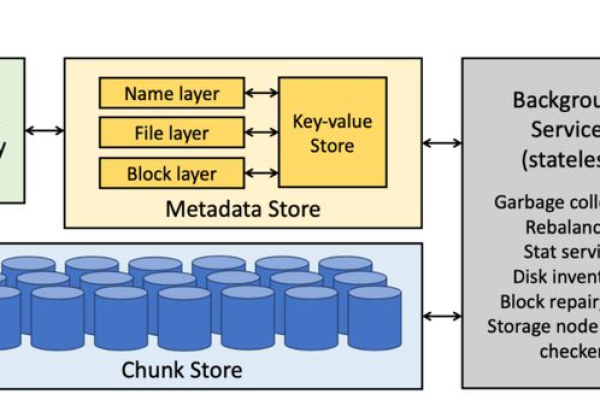
大型分布式网站的架构通常采用分层的模式,包括应用层、服务层、数据层、管理层和分析层,每一层都有其特定职责,如应用层负责前端展示逻辑,服务层处理业务逻辑,数据层管理数据存储和检索等,根据业务或功能模块的特点进行水平或垂直分割,有助于提升系统的灵活性和可维护性。
在技术选型上,分布式消息系统如Kafka扮演着重要的角色,它通过分布式、分区、多副本的特性来满足大规模数据处理的需求,支持实时处理和流式处理等多种场景,Kafka基于Zookeeper进行协调,确保了消息系统的高可用性和一致性。
【性能与高可用性策略】
为了保障大型分布式网站的性能,各层级都需实施优化措施,在应用层使用CDN分发静态资源减少延迟;服务层利用微服务架构和解耦来提升系统的伸缩性和容错能力;数据层则采用数据库分库分表、缓存策略等来提高数据处理速度。
高可用性策略涉及冗余部署、负载均衡和服务熔断等机制,冗余部署可以保证当某个节点发生故障时,其他节点能够继续提供服务,负载均衡则将请求合理分配到多个服务器上,避免单点压力过大造成崩溃,服务熔断机制能在检测到异常时快速切断故障服务的调用,防止故障蔓延。
【安全性与扩展性考量】
安全性是大型分布式网站架构中不可忽视的部分,常见的安全措施包括数据加密传输、用户认证授权、网络防火墙、载入检测系统等,扩展性则要求架构允许快速添加或去除功能模块,这通常通过服务化架构和解耦合的设计来实现。
【敏捷响应与运维监控】
大型分布式网站需要敏捷地响应市场和技术的变化,敏捷性体现在持续集成和持续部署(CI/CD)流程的效率,以及团队对变化需求的快速响应能力上,良好的运维监控体系是确保网站稳定运行的关键,它能实时监控系统状态,及时发现并处理问题。
【相关问答FAQs】
1、什么是微服务架构?
微服务架构是一种将单一应用程序开发为一套小服务的方法,每个服务运行在其独立的进程中,并通过轻量级的通信机制(通常是HTTP资源API)互相协作,这种架构使得服务可以独立部署、扩展和升级,提高了大型分布式网站的灵活性和可维护性。
2、如何实现大型分布式网站的数据一致性?
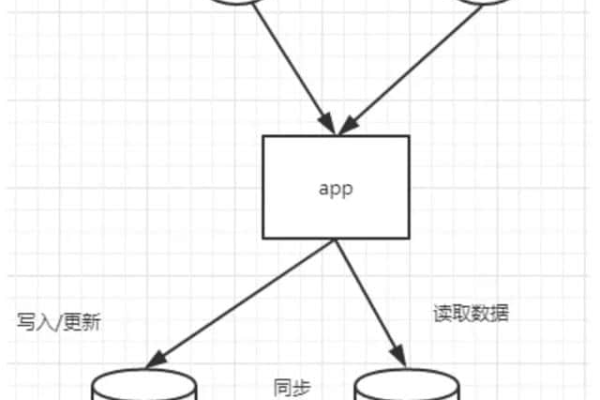
数据一致性可以通过多种方式实现,包括但不限于:使用分布式事务协议来保证跨服务的数据操作原子性;利用事件驱动架构和分布式消息系统如Kafka进行服务间的数据同步;以及采用数据网格(Data Mesh)架构理念,将数据视为一种产品,按照领域能力进行划分和管理。