对象存储新建文件夹_新建文件夹
- 行业动态
- 2024-07-09
- 2
在众多云服务平台中,对象存储服务(Object Storage Service, OSS)以其高可靠性、易扩展性和成本效率而受到企业的青睐,尽管对象存储采用扁平化结构存储数据,与传统文件系统不同,但它依然能够通过特定方式实现类似文件夹的功能,以适应用户的操作习惯,下面将详细解析在对象存储中新建“文件夹”的具体操作步骤,并探讨其背后的技术原理及使用场景。
1、登录和导航至正确位置:用户需要登录到相应的云平台控制台,进入对象存储的管理界面,以京东云为例,用户需进入空间管理,在空间列表中选择任意一个存储空间。
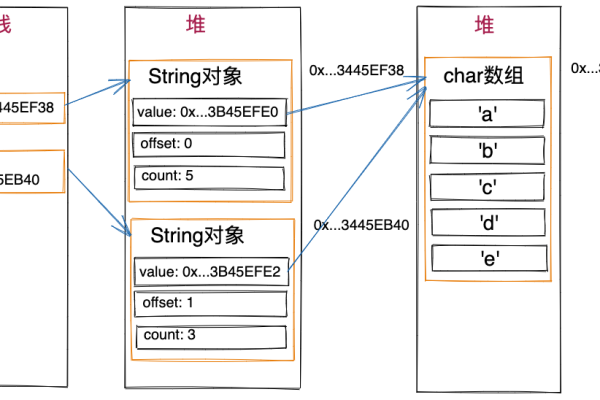
2、理解对象存储的结构:对象存储内部是以扁平结构存储数据的,所有数据均以对象(Object)的形式保存在存储空间(Bucket)中,这种结构没有传统意义上的文件夹概念,而是通过在对象键(Key)中使用‘/’字符作为后缀来模拟文件夹。
3、新建“文件夹”:在选定的存储空间内,用户可以选择新建“文件夹”,这一操作实际上是创建了一个存储空间为0KB的对象,其命名符合所设定的规则,并以‘/’结束,从而在视觉上呈现出文件夹的效果。
4、使用场景:新建“文件夹”可以帮助用户更好地分类和管理存储在OSS中的数据,可以在已创建的桶中新建一个“文件夹”,以便更有效地组织数据,如文档、图片等。
虽然上述步骤基于特定的云平台进行描述,但大多数对象存储服务的基本原理和操作步骤是相似的,了解这些细节可以帮助用户更高效地利用对象存储服务进行数据管理。
相关问答FAQs
Q1: 对象存储中的“文件夹”是否占用存储空间?
A1: 是的,对象存储中的“文件夹”实际上是一种特殊类型的对象,它占用非常小的存储空间(0KB),这是因为它们主要作为组织其他对象的容器存在。
Q2: 如何删除对象存储中的“文件夹”?
A2: 删除“文件夹”实际上意味着删除该对象,由于“文件夹”本身是一个对象(以‘/’结尾的键名标识),因此直接删除该对象即可,需要注意的是,这也会同时删除该“文件夹”中所有的子对象,除非采取特定措施仅移除“文件夹”对象本身而不删除其内容。
归纳而言,虽然对象存储系统内部采用扁平化结构,但通过特定的命名规则和对象操作,用户可以模拟出类似于传统文件系统的文件夹功能,掌握新建“文件夹”的操作步骤及其背后的技术原理,能够帮助用户更有效地管理和组织在云平台上的数据。