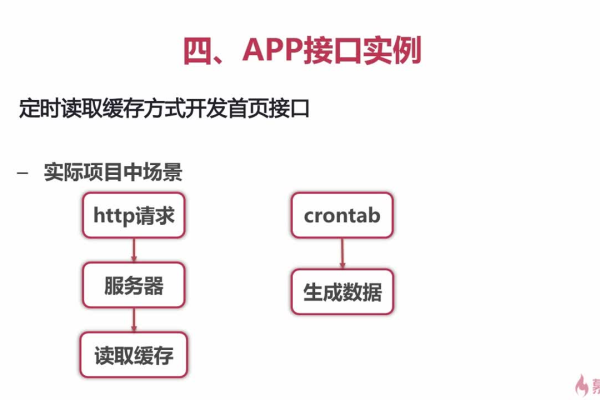
c api接口开发实例

在C语言中开发API接口是一项复杂但至关重要的任务，它涉及到多个方面的技术和设计考量，以下是关于C API接口开发的详细实例：

1、定义清晰的接口规范

函数命名：采用“模块_功能”的命名方式，使用户能直观理解函数用途，例如文件处理模块的函数file_open、file_close、file_read、file_write等。

参数类型及含义：明确参数类型，并在注释中详细说明含义，如file_open函数的参数const char *filename表示要打开的文件名。

返回值和错误码：定义明确的返回值和错误码，通常函数返回0表示成功，非零值表示错误，错误码定义为宏以提高可读性和维护性，如#define FILE_SUCCESS 0、#define FILE_ERROR -1。

2、确保接口的稳定性和向后兼容性

避免破坏性修改：添加新功能时，避免修改已有函数签名或行为，可通过增加新函数实现，例如在文件操作API中，若需增加以特定模式打开文件的功能，可新增file_open_ex函数。

使用版本管理：接口变更时使用版本管理机制，在头文件中定义版本号，以便用户选择合适的版本。

3、提供详尽的文档和示例代码

功能：简要介绍API的功能和用途，帮助用户快速了解其作用。

函数说明：每个函数应有详细参数、返回值和可能错误码的说明，并提供示例代码展示正确使用方法，如file_write函数的示例代码展示了如何使用该函数向文件写入数据。

常见问题解答（FAQ）：文档中包含常见问题解答，帮助用户解决常见问题，例如解释file_open返回-1的原因，以及如何处理file_write返回的错误。

4、实际示例

头文件（file_api.h）

     #ifndef FILE_API_H
     #define FILE_API_H
     #include <stddef.h>
     #define FILE_SUCCESS 0
     #define FILE_ERROR -1
     #ifdef __cplusplus
     extern "C" {
     #endif
     /* Open a file */
     int file_open(const char *filename);
     /* Close a file */
     int file_close(int file_descriptor);
     /* Read data from a file */
     int file_read(int file_descriptor, void *buffer, size_t size);
     /* Write data to a file */
     int file_write(int file_descriptor, const void *buffer, size_t size);
     #ifdef __cplusplus
     }
     #endif
     #endif // FILE_API_H

源文件（file_api.c）

     #include "file_api.h"
     #include <fcntl.h>
     #include <unistd.h>
     #include <string.h>
     #include <errno.h>
     /* Open a file */
     int file_open(const char *filename) {
         int fd = open(filename, O_RDWR | O_CREAT, S_IRUSR | S_IWUSR);
         if (fd == -1) {
             return FILE_ERROR;
         }
         return fd;
     }
     /* Close a file */
     int file_close(int file_descriptor) {
         if (close(file_descriptor) == -1) {
             return FILE_ERROR;
         }
         return FILE_SUCCESS;
     }
     /* Read data from a file */
     int file_read(int file_descriptor, void *buffer, size_t size) {
         ssize_t bytes_read = read(file_descriptor, buffer, size);
         if (bytes_read == -1) {
             return FILE_ERROR;
         }
         return (int)bytes_read;
     }
     /* Write data to a file */
     int file_write(int file_descriptor, const void *buffer, size_t size) {
         ssize_t bytes_written = write(file_descriptor, buffer, size);
         if (bytes_written == -1) {
             return FILE_ERROR;
         }
         return (int)bytes_written;
     }

测试文件（main.c）

     #include "file_api.h"
     #include <stdio.h>
     int main() {
         int fd = file_open("example.txt");
         if (fd != FILE_ERROR) {
             const char *data = "Hello, World!";
             size_t bytes_written = file_write(fd, data, strlen(data));
             if (bytes_written == -1) {
                 printf("Write error: %s
", strerror(errno));
             } else {
                 printf("Written %zu bytes.
", bytes_written);
             }
             file_close(fd);
         } else {
             printf("Failed to open file.
");
         }
         return 0;
     }

相关问答FAQs

1、问：为什么file_open函数返回FILE_ERROR？

答：可能的原因包括文件不存在、没有权限访问文件或文件名无效，请检查文件路径和权限。

2、问：如何处理file_write返回的错误？

答：如果file_write返回FILE_ERROR，应检查errno以确定错误原因，可能的错误包括磁盘已满、文件描述符无效等。

小编有话说

C API接口开发需要严谨的设计和实现，以确保接口的高效性、稳定性和易用性，在实际开发中，应根据具体需求进行合理的设计和优化，为用户提供高质量的API服务。