如何应对头条广告账户起量波动?专业操作指南解析
- 行业动态
- 2024-09-10
- 3
在面对头条投放账户起量不稳定的问题时,采取一系列有针对性的措施是至关重要的,以下是一些详细的步骤指导,旨在帮助您优化账户性能,实现稳定的广告投放效果。
数据分析与诊断
1. 分析账户历史数据
回顾过去一段时间内的广告表现,包括点击率、转化率、消耗速度等关键指标。
识别出表现不佳的广告或广告组,并记录下相关特征。
2. 定位问题原因
检查广告定向设置是否过于狭窄或过于宽泛,影响广告覆盖范围。
分析创意内容是否存在吸引力不足或与目标受众不匹配的情况。
评估出价策略是否合理,是否存在出价过低导致广告曝光不足的问题。
优化广告定向
1. 调整目标人群
根据之前的数据分析结果,重新设定更精准的目标人群定向。
考虑使用相似受众或扩展定向特征以增加潜在触达。
2. 多维度测试
对不同的受众群体进行A/B测试,找出响应最好的受众特征。
测试不同的兴趣、行为标签组合,优化目标精准度。
创意和素材优化
1. 更新创意内容
定期更新广告文案和图片/视频素材,保持新鲜感,提高用户兴趣。
尝试不同的广告形式,比如视频、动态图等,以提高互动性。
2. 测试创意效果
对各种创意进行轮播测试,分析哪些元素(如颜色、布局、文案)最受目标受众欢迎。
优化点击率低的创意,并复制高效创意的元素到其他广告中。
出价策略调整
1. 分析竞价环境
了解行业平均水平和竞争对手的出价策略。

判断是否需要调整CPC或CPM出价,以便在竞争中占据优势。
2. 实施动态出价
利用头条平台提供的自动化工具,如智能出价或目标每次转化费用(CPA)出价策略。
定期检查并调整出价,确保广告维持合理的曝光和转化。
持续监控与优化
1. 实时监控广告表现
利用头条广告后台的数据监控功能,实时跟踪广告投放的各项指标。
快速响应广告表现变化,及时做出调整。
2. 长期优化计划
建立长期的优化日程,包括定期的数据分析和广告调整。
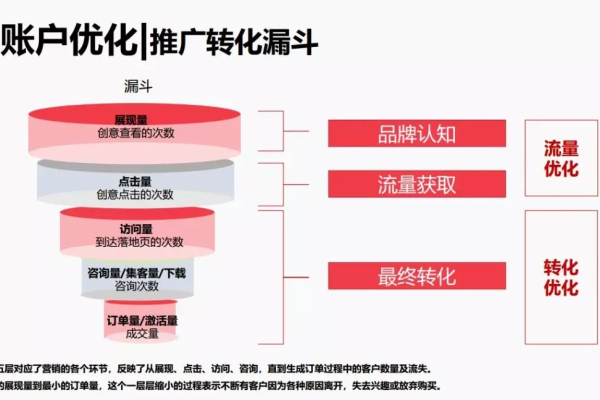
归纳成功案例和失败教训,形成经验,指导下一次的广告投放。
在接下来的部分,我们添加了一些相关的FAQs,以帮助解决更多关于头条投放账户操作的疑问。
常见问题解答
Q1: 广告投放初期无点击怎么办?
确保您的广告定向准确,并且创意吸引人,初期可尝试提高出价,以获得更好的曝光机会,分析竞争对手的广告策略,看看是否有可以借鉴的地方,如果问题依旧,不妨更换新的创意或尝试不同的受众群体。
Q2: 如何提升广告的转化率?
转化率提升需要从多个方面努力,确保落地页面与广告承诺一致,优化用户体验,减少页面加载时间,细分受众并进行针对性的创意设计,确保广告对于观看的人群具有吸引力,不断测试不同的广告元素和文案,找到最能促进转化的组合。








