逻辑运算法则是什么?
- 行业动态
- 2024-11-10
- 2020
逻辑运算法则包括与、或、非等基本操作,用于处理布尔值。
逻辑运算法则
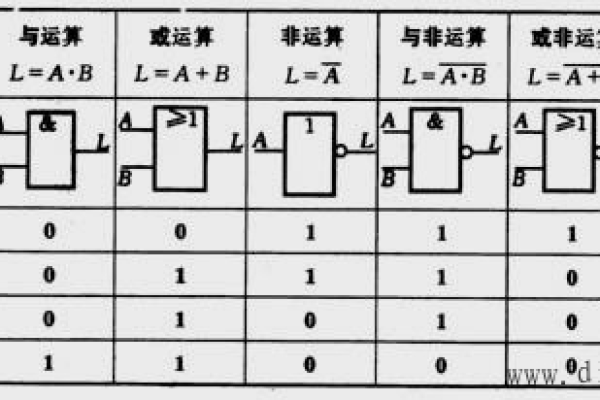
逻辑运算是计算机科学和数学中的基本概念,用于处理布尔值(真或假),这些运算在数字电路设计、编程和算法开发等领域有着广泛的应用,本文将详细介绍几种基本的逻辑运算法则:与(AND)、或(OR)、非(NOT)、异或(XOR)以及它们的组合应用。
1. 与运算(AND)
定义
与运算是一种二元操作符,只有当两个输入都为真时,输出才为真;否则为假。
真值表
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
应用场景
在编程中,可以用来检查多个条件是否同时满足。
在硬件设计中,用于实现多路信号的选择。
2. 或运算(OR)
定义
或运算也是一种二元操作符,只要有一个输入为真,输出就为真;如果两个输入都为假,输出为假。
真值表
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
应用场景
在编程中,用于至少一个条件成立的情况下执行某些操作。
在硬件设计中,用于实现多路信号的合并。
3. 非运算(NOT)
定义
非运算是一元操作符,它将输入的布尔值取反。
真值表
| A | NOT A |
| 0 | 1 |
| 1 | 0 |
应用场景
在编程中,用来反转条件判断的结果。
在硬件设计中,用于生成相反的信号状态。
4. 异或运算(XOR)
定义
异或运算是一种二元操作符,当两个输入不同时,输出为真;当两个输入相同时,输出为假。
真值表
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
应用场景
在编程中,用于检测两个变量是否不同。
在硬件设计中,用于实现简单的加法器等算术单元。
5. 逻辑运算的组合应用
逻辑运算可以通过不同的组合来实现更复杂的逻辑功能,使用与、或和非运算可以构建出任何逻辑函数,以下是一些常见的组合形式及其用途:
NAND 运算
NAND 是与运算的否定,即A NAND B = NOT (A AND B),NAND 门是所有逻辑门的基础,因为任何其他类型的逻辑门都可以用 NAND 门来构造。
NOR 运算
NOR 是或运算的否定,即A NOR B = NOT (A OR B),同样地,NOR 门也是通用的逻辑门之一。
XNOR 运算
XNOR 是异或运算的否定,即A XNOR B = NOT (A XOR B),XNOR 运算通常用于比较两个二进制数是否相等。
6. 逻辑运算在数字电路中的应用
逻辑运算广泛应用于数字电路的设计中,如触发器、计数器、寄存器等,通过组合基本的逻辑门,可以构建出复杂的数字系统,一个简单的 D 触发器可以用四个 NAND 门来实现。
7. 逻辑运算在编程中的应用
在编程语言中,逻辑运算符通常用于控制流程语句中的条件表达式,在 C++ 语言中,可以使用&& 表示与运算,|| 表示或运算,! 表示非运算,这些运算符可以帮助程序员编写更加灵活和强大的代码。
8. 逻辑运算在算法中的应用
逻辑运算在算法设计中也扮演着重要的角色,在搜索算法中,可以使用逻辑运算来判断某个节点是否满足特定的条件;在排序算法中,可以使用逻辑运算来确定两个元素的顺序关系。
9. 逻辑运算的优化技巧
在实际的应用中,为了提高性能和效率,经常需要对逻辑运算进行优化,以下是一些常见的优化技巧:
短路求值:对于与运算和或运算,一旦确定了最终结果,就可以提前终止计算,对于A && B,如果A 为假,则不需要再计算B;对于A || B,如果A 为真,则不需要再计算B。
消除冗余:在逻辑表达式中,有时会出现重复计算的情况,通过重新组织表达式,可以避免这种冗余,将A && A 简化为A。
使用德摩根定律:德摩根定律指出,对于任何布尔表达式F,有NOT (F) = (NOT F),利用这一定律可以将复杂的逻辑表达式转换为更简单的形式,将NOT (A AND B) 转换为NOT A OR NOT B。
FAQs
Q1: 什么是短路求值?它如何工作?
A1: 短路求值是一种编程技术,用于在逻辑表达式的求值过程中跳过不必要的计算,对于与运算(AND),如果第一个操作数为假,则整个表达式的结果必然为假,因此无需计算第二个操作数;对于或运算(OR),如果第一个操作数为真,则整个表达式的结果必然为真,因此无需计算第二个操作数,这种技术可以提高程序的运行效率。
Q2: 如何使用德摩根定律来简化逻辑表达式?
A2: 德摩根定律指出,对于任何布尔表达式F,有NOT (F) = (NOT F),这意味着我们可以通过对逻辑表达式取反并将其内部的与、或运算互换位置来简化表达式,假设我们有以下逻辑表达式:NOT (A AND B),根据德摩根定律,我们可以将其转换为NOT A OR NOT B,这样不仅简化了表达式,还可能减少了计算量。
以上内容就是解答有关“逻辑运算法则”的详细内容了,我相信这篇文章可以为您解决一些疑惑,有任何问题欢迎留言反馈,谢谢阅读。
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/102551.html